
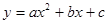 的顶点为P,抛物线:与y轴交于点A,与直线OP交于点B.过点P作PD⊥x轴于点D,平移抛物线F使其经过点A、D得到抛物线F′:
的顶点为P,抛物线:与y轴交于点A,与直线OP交于点B.过点P作PD⊥x轴于点D,平移抛物线F使其经过点A、D得到抛物线F′: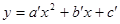 ,抛物线F′与x轴的另一个交点为C.
,抛物线F′与x轴的另一个交点为C.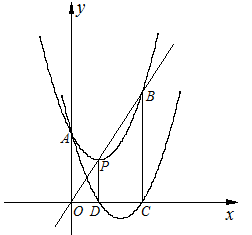
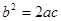
 ,令
,令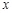 =0,则
=0,则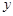 =
=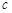 ,
, 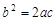 ,∴
,∴ 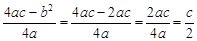 ,
,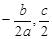 ).
). 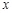 轴于D,∴点D的坐标为(
轴于D,∴点D的坐标为(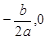 ).
).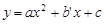 .
.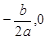 ),∴
),∴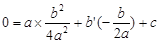 .
.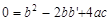 .
.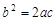 ,∴
,∴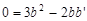 .
.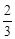 .
.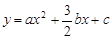 .
.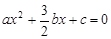 .
.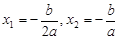 .
. ∴点C的坐标为(
∴点C的坐标为(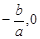 ).
). 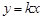 .
.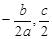 ),
), ,∴
,∴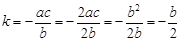 ,∴
,∴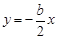 .
.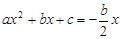 .
.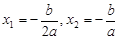 .
.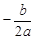 ,∴点B的横坐标为
,∴点B的横坐标为 .
.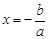 代入
代入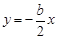 ,得
,得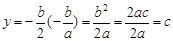 .
.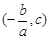 .
.

科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
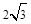 ,0)作圆B的切线交圆于点P,已知tan∠PAB=
,0)作圆B的切线交圆于点P,已知tan∠PAB=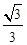 ,抛物线C经过A、P两点。
,抛物线C经过A、P两点。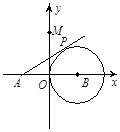
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,
, ),且点B关于原点的对称点C也在该抛物线上.
),且点B关于原点的对称点C也在该抛物线上. 的点共有 个;
的点共有 个;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,对角线AC与BD相交于O,AB=8cm,AD=10cm,BC=6cm,一个动点E从点B出发,以每秒1cm的速度沿射线BA方向移动,过E作EQ⊥AB,交直线AC于P,交直线BD于Q,以PQ为边向上作正方形PQMN,设正方形PQMN与△BOC,重叠部分的面积为s,点E的运动时间为t秒.
,对角线AC与BD相交于O,AB=8cm,AD=10cm,BC=6cm,一个动点E从点B出发,以每秒1cm的速度沿射线BA方向移动,过E作EQ⊥AB,交直线AC于P,交直线BD于Q,以PQ为边向上作正方形PQMN,设正方形PQMN与△BOC,重叠部分的面积为s,点E的运动时间为t秒.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
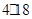 烟花三月经贸旅游节特别设计制作一种新型礼炮,这种礼炮的升空高度
烟花三月经贸旅游节特别设计制作一种新型礼炮,这种礼炮的升空高度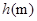 与飞行时间
与飞行时间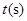 的关系式是
的关系式是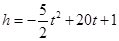 ,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为( )
,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为( )A.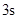 | B.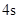 | C.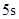 | D.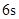 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
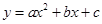 的图象如图所示,给出下列说法:
的图象如图所示,给出下列说法: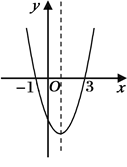
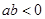 ;②方程
;②方程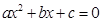 的根为
的根为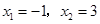 ;
;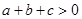 ;④当
;④当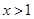 时,y随x值的增大而增大;
时,y随x值的增大而增大; 时,
时,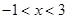 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com