
【题目】已知,正方形![]() 中,点E在
中,点E在![]() 上,点F在
上,点F在![]() 上,连接
上,连接![]() 、
、![]() 、
、![]() .且
.且![]() 平分
平分![]() .
.

(1)如图1,求证:![]() .
.
(2)如图2,若点E为BC的中点,![]() ,求
,求![]() 的面积.
的面积.
(3)如图3,若∠B=90°,连接BD分别交AF、AE于M、N两点,连接ME,若ME⊥AF于M, BM:EF=4![]() :5,△AEF的面积为15时,求AE的长度.
:5,△AEF的面积为15时,求AE的长度.
【答案】(1)证明见解析;(2)15;(3)2![]() .
.
【解析】
(1)作AH⊥EF于H.只要证明△AFD≌△AFH,推出∠FAD=∠FAH,同法可证:∠EAB=∠EAH,由此即可解决问题;
(2)由△EAB≌△EAH,△FAD≌△FAH,推出BE=EH=3,DF=FH,设DF=FH=x,在Rt△EFC中,根据EF2=EC2+CF2,可得(x+3)2=32+(6-x)2,推出x=2,推出EF=3+2=5,即可解决问题;
(3)如图3中,如图将△ADM顺时针旋转90°得到△ABK.首先证明MN2=BN2+DM2,再证明EF=![]() MN,由BM:EF=4
MN,由BM:EF=4![]() :5,推出BM:
:5,推出BM:![]() MN=4
MN=4![]() :5,推出BM:NM=8:5,设BM=8k,NM=5k,则BN=3k,DM=
:5,推出BM:NM=8:5,设BM=8k,NM=5k,则BN=3k,DM=![]() =4k,由DF∥AB,推出
=4k,由DF∥AB,推出![]() =2,设MF=y,则AM=ME=2y,由
=2,设MF=y,则AM=ME=2y,由![]() AFEM=15,推出
AFEM=15,推出![]() 3b2b=15,可得b=
3b2b=15,可得b=![]() ,由此即可解决问题.
,由此即可解决问题.
(1)证明:作AH⊥EF于H.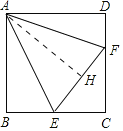
∵四边形ABCD是正方形,
∴∠B=∠D=∠BAD=90°,AB=AD=BC=CD,
∵AE平分∠BEF,AB⊥BE,AH⊥EF,
∴AB=AH=AD,
在Rt△AFD和Rt△AFH中,![]() ,
,
∴△AFD≌△AFH,
∴∠FAD=∠FAH,同法可证:∠EAB=∠EAH,
∴∠EAF=![]() ∠BAH+
∠BAH+![]() ∠DAH=
∠DAH=![]() ×90°=45°.
×90°=45°.
(2)解:∵△EAB≌△EAH,△FAD≌△FAH,
∴BE=EH=3,DF=FH,设DF=FH=x,
在Rt△EFC中,∵EF2=EC2+CF2,
∴(x+3)2=32+(6-x)2,
∴x=2,
∴EF=3+2=5,
∴S△AEF=![]() ×5×6=15.
×5×6=15.
(3)解:如图3中,如图将△ADM顺时针旋转90°得到△ABK.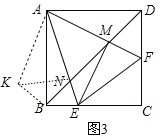
∵∠BAD=90°,∠MAN=45°,
∴∠DAM+∠BAN=45°,
∵∠DAM=∠BAK,
∴∠BAN+∠BAK=45°,
∴∠NAK=∠MAN=45°,
∵AN=AN,AK=AM,
∴△ANK≌△ANM,
∴MN=KN,
∵∠ABK=∠ADM=45°=∠ABD,
∴∠KBN=90°,
∴KN2=BN2+BK2,
∵DM=BK,
∴MN2=BN2+DM2,
∵∠MAN=∠NBE,∠ANM=∠BNE,
∴∠AMN=∠BEN=∠AEF,
∵∠AMN=∠EAF,
∴△AMN∽△AEF,
∴![]() ,
,
∴EF=![]() MN,
MN,
∵BM:EF=4![]() :5,
:5,
∴BM:![]() MN=4
MN=4![]() :5,
:5,
∴BM:NM=8:5,设BM=8k,NM=5k,
则BN=3k,DM=![]() =4k,
=4k,
∵DF∥AB,
∴![]() =2,设MF=y,则AM=ME=2y,
=2,设MF=y,则AM=ME=2y,
∵![]() AFEM=15,
AFEM=15,
∴![]() 3b2b=15,
3b2b=15,
∴b2=5,
∵b>0,
∴b=![]() ,
,
∴AM=EM=2![]() ,
,
∴AE=![]() AM=2
AM=2![]() .
.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
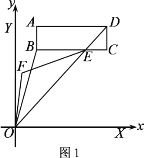
【题目】如图,长方形ABCD在平面直角坐标系中,点A(1,8),B(1,6),C(7,6),点X,Y分别在x,y轴上.
(1)请直接写出D点的坐标 ;
(2)连接OB、OD,OD交BC于点E,∠BOY的平分线和∠BEO的平分线交于点F,若∠BOE=n,求∠OFE的度数.
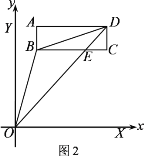
(3)若长方形ABCD以每秒![]() 个单位的速度向下运动,设运动时间为t秒,问在第一象限内是否存在某一时刻t,使△OBD的面积等于长方形ABCD的面积的
个单位的速度向下运动,设运动时间为t秒,问在第一象限内是否存在某一时刻t,使△OBD的面积等于长方形ABCD的面积的![]() ?若存在,请求出t的值,若不存在,请说明理由。
?若存在,请求出t的值,若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (m>0)与x轴交于A、B两点.
(m>0)与x轴交于A、B两点.
(1)求证:抛物线的对称轴在y轴的左侧;
(2)若![]() (O为坐标原点),求抛物线的解析式;
(O为坐标原点),求抛物线的解析式;
(3)设抛物线与y轴交于点C,若△ABC是直角三角形.求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两队进行拔河比赛,裁判员让两队队长用“石头、剪子、布”的手势方式选择场地位置.规则是:石头胜剪子,剪子胜布,布胜石头,手势相同再决胜负.请你说明裁判员的这种作法对甲、乙双方是否公平,为什么?(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场设立了一个可以自由转动的转盘,并做如下规定:顾客购物80元以上就获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品,下表是活动进行中的一组统计数据.

(1)计算并完成表格;
(2)请估计,当n很大时,频率将会接近多少?
(3)假如你去转动该盘一次,你获得洗衣粉的概率约是多少?
(4)在该转盘中,表示“洗衣粉”区域的扇形的圆心角约是多少?(精确到1°)
查看答案和解析>>
科目:初中数学 来源: 题型:
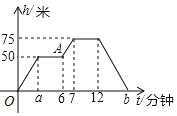
【题目】某次大型活动,组委会启用无人机航拍活动过程,在操控无人机时应根据现场状况调节高度,已知无人机在上升和下降过程中速度相同,设无人机的飞行高度h(米)与操控无人机的时间t(分钟)之间的关系如图中的实线所示,根据图象回答下列问题:
(1)图中的自变量是______,因变量是______;
(2)无人机在75米高的上空停留的时间是______分钟;
(3)在上升或下降过程中,无人机的速度______为米/分;
(4)图中a表示的数是______;b表示的数是______;
(5)图中点A表示______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图表示甲骑摩托车和乙驾驶汽车沿相同的路线行驶90千米,由A地到B地时,行驶的路程y(千米)与经过的时间x(小时)之间的关系。请根据图象填空:
(1)摩托车的速度为_____千米/小时;汽车的速度为_____千米/小时;
(2)汽车比摩托车早_____小时到达B地。
(3)在汽车出发后几小时,汽车和摩托车相遇?说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com