
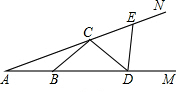
 如图,点B,D在射线AM上,点C,E在射线AN上,且AB=BC=CD=DE,已知∠EDM=84°,求∠A的度数.
如图,点B,D在射线AM上,点C,E在射线AN上,且AB=BC=CD=DE,已知∠EDM=84°,求∠A的度数.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
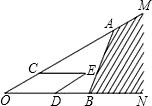 如图,点A,B分别在射线OM,ON上,C,D分别是线段OA和OB上的点,以OC,OD为邻边作平行四边形OCED,下面给出三种作法的条件:①取OC=
如图,点A,B分别在射线OM,ON上,C,D分别是线段OA和OB上的点,以OC,OD为邻边作平行四边形OCED,下面给出三种作法的条件:①取OC=| 3 |
| 4 |
| 3 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
| 4 |
| 1 |
| 5 |
| A、① | B、①② | C、①②③ | D、②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:
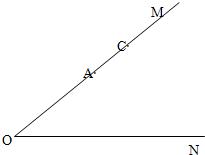 24、已知∠MON如图,点A、C在射线OM上,请按要求完成下列作图(保留画图痕迹)及证明
24、已知∠MON如图,点A、C在射线OM上,请按要求完成下列作图(保留画图痕迹)及证明查看答案和解析>>
科目:初中数学 来源: 题型:
| k | x |

查看答案和解析>>
科目:初中数学 来源:2014年中考数学二轮精品复习开放型问题练习卷(解析版) 题型:解答题
(1)先求解下列两题:
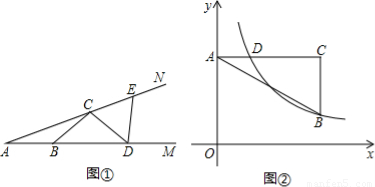
①如图①,点B,D在射线AM上,点C,E在射线AN上,且AB=BC=CD=DE,已知∠EDM=84°,求∠A的度数;
②如图②,在直角坐标系中,点A在y轴正半轴上,AC∥x轴,点B,C的横坐标都是3,且BC=2,点D在AC上,且横坐标为1,若反比例函数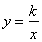 (x>0)的图象经过点B,D,求k的值.
(x>0)的图象经过点B,D,求k的值.
(2)解题后,你发现以上两小题有什么共同点?请简单地写出.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com