
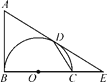
【题目】如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD,BC的延长线相交于点E.
(1)求证:AD是半圆O的切线;
(2)连结CD,求证:∠A=2∠CDE;
【答案】证明见解析
【解析】
(1)如图,连接OD,BD,
∵AB是⊙O的切线,∴AB⊥BC,即∠ABC=90°,
∵AB=AD,∴∠ABD=∠ADB,
∵OB=OD,∴∠DBO=∠BDO,∴∠ABD+∠DBO=∠ADB+∠BDO,
∴∠ADO=∠ABO=90°,∴AD是半圆O的切线.
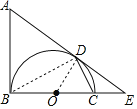
(2)由(1)知,∠ADO=∠ABO=90°,
∴∠A=360°–∠ADO–∠ABO–∠BOD=180°–∠BOD=∠DOC,
∵AD是半圆O的切线,∴∠ODE=90°,∴∠ODC+∠CDE=90°,
∵BC是⊙O的直径,∴∠ODC+∠BDO=90°,∴∠BDO=∠CDE,
∵∠BDO=∠OBD,∴∠DOC=2∠BDO,∴∠DOC=2∠CDE,
∴∠A=2∠CDE.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
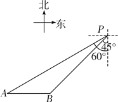
【题目】如图,一艘轮船位于灯塔P南偏西60°方向的A处,它向东航行20海里到达灯塔P南偏西45°方向上的B处,若轮船继续沿正东方向航行,求轮船航行途中与灯塔P的最短距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
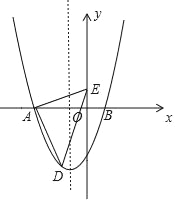
【题目】如图,在平面直角坐标系中,二次函数y=ax2+bx﹣3交x轴于点A(﹣3,0)、B(1,0),在y轴上有一点E(0,1),连接AE.
(1)求二次函数的表达式;
(2)若点D为抛物线在x轴负半轴下方的一个动点,求△ADE面积的最大值;
(3)抛物线对称轴上是否存在点P,使△AEP为等腰三角形?若存在,请直接写出所有P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣x2+mx+n交x轴于点A(﹣2,0)和点B,交y轴于点C(0,2).
(1)求抛物线的函数表达式;
(2)若点M在抛物线上,且S△AOM=2S△BOC,求点M的坐标;
(3)如图2,设点N是线段AC上的一动点,作DN⊥x轴,交抛物线于点D,求线段DN长度的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更好地开展选修课,戏剧社的张老师统计了近五年该社团学生参加市级比赛的获奖情况,并绘制成如下两幅不完整的统计图,请根据图中的信息,完成下列问题:

![]() 该社团2017年获奖学生人数占近五年获奖总人数的百分比为_____,补全折线统计图;
该社团2017年获奖学生人数占近五年获奖总人数的百分比为_____,补全折线统计图;
![]() 该社团2017年获奖学生中,初一、初二年级各有一名学生,其余全是初三年级学生,张老师打算从2017年获奖学生中随机抽取两名学生参加学校的艺术节表演,请你用列表法或画树状图的方法,求出所抽取两名学生恰好都来自初三年级的概率.
该社团2017年获奖学生中,初一、初二年级各有一名学生,其余全是初三年级学生,张老师打算从2017年获奖学生中随机抽取两名学生参加学校的艺术节表演,请你用列表法或画树状图的方法,求出所抽取两名学生恰好都来自初三年级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:
①abc<0;②![]() >0;③ac﹣b+1=0;④OAOB=﹣
>0;③ac﹣b+1=0;④OAOB=﹣![]() .
.
其中正确结论的个数是( )

A.4 B.3 C.2 D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
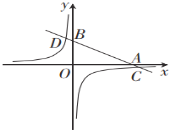
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象分别交x轴、y轴于A、B两点,与反比例函数
的图象分别交x轴、y轴于A、B两点,与反比例函数![]() 的图象交于C、D两点.已知点C的坐标是(6,-1),D(n,3).
的图象交于C、D两点.已知点C的坐标是(6,-1),D(n,3).
(1)求m的值和点D的坐标.
(2)求![]() 的值.
的值.
(3)根据图象直接写出:当x为何值时,一次函数的值大于反比例函数的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
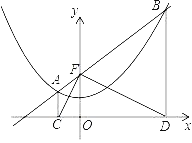
【题目】如图,动直线 y=kx+2(k>0)与 y 轴交于点 F,与抛物线 y=![]() 相交于A,B 两点,过点 A,B 分别作 x 轴的垂线,垂足分别为点 C,D,连接 CF,DF,请你判断△CDF 的形状,并说明理由.
相交于A,B 两点,过点 A,B 分别作 x 轴的垂线,垂足分别为点 C,D,连接 CF,DF,请你判断△CDF 的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com