
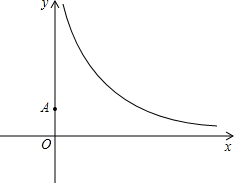
 已知双曲线y=$\frac{k}{x}$(x>0)经过点(2,3$\sqrt{3}$).
已知双曲线y=$\frac{k}{x}$(x>0)经过点(2,3$\sqrt{3}$).分析 (1)根据待定系数法即可求得;
(2)解直角三角形求得AB=2$\sqrt{3}$,根据等边三角形的性质求得PB=2$\sqrt{3}$,将PB=2$\sqrt{3}$代入函数的解析式后求得x的值即可作为P点的横坐标,从而求得P点的纵坐标;
(3)分两种情况分别讨论即可求得.
解答 解:(1)∵双曲线y=$\frac{k}{x}$(x>0)经过点(2,3$\sqrt{3}$),
∴3$\sqrt{3}$=$\frac{k}{2}$,
解得:k=6$\sqrt{3}$;
故答案为:6$\sqrt{3}$;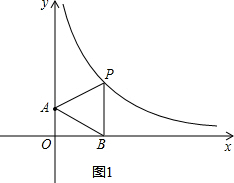
(2)如图1,∵△PAB等边三角形,
∴∠PBA=60°,PB=AB,
∵PB⊥x轴,
∴∠ABO=30°,
∴AB=2OA=2$\sqrt{3}$,
∴OB=$\sqrt{A{B}^{2}-O{A}^{2}}$=3,
∴PB=AB=2$\sqrt{3}$,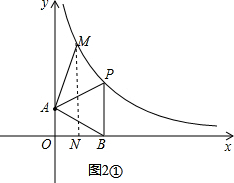 ∴点P的坐标为:(3,2$\sqrt{3}$);
∴点P的坐标为:(3,2$\sqrt{3}$);
(3)设M的坐标为(m,$\frac{6\sqrt{3}}{m}$),
作MN⊥x轴于N,
当0<m<3时,如图2①,
∵S梯形AMNO+S梯形PMNB-S△AOB=2S△PAB,
∴m($\sqrt{3}$+$\frac{6\sqrt{3}}{m}$)+(3-m)(2$\sqrt{3}$+$\frac{6\sqrt{3}}{m}$)-3×$\sqrt{3}$=2×3×$2\sqrt{3}$,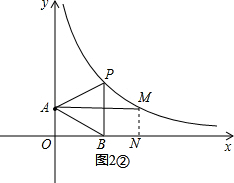
整理得,m2+9m-18=0,
解得m1=$\frac{-9+3\sqrt{17}}{2}$,m2=$\frac{-9-3\sqrt{17}}{2}$(舍去),
∴M($\frac{-9+3\sqrt{17}}{2}$,$\frac{3\sqrt{3}+\sqrt{51}}{2}$);
当m>3时,如图2②,
∵S梯形AOBP+S梯形PMNB-S△AOB=2S△PAB,
则3($\sqrt{3}$+2$\sqrt{3}$)+(m-3)(2$\sqrt{3}$+$\frac{6\sqrt{3}}{m}$)-3×$\sqrt{3}$=2×3×$2\sqrt{3}$,
整理得,m2-3m-9=0,
解得,m3=$\frac{3+3\sqrt{5}}{2}$,m4=$\frac{3-3\sqrt{5}}{2}$(舍去),
∴M($\frac{3+3\sqrt{5}}{2}$,$\sqrt{15}$-$\sqrt{3}$).
点评 本题是反比例函数的综合题,考查了待定系数法,等边三角形的性质,解直角三角形,梯形的面积等,(3)根据S梯形AMNO+S梯形PMNB-S△AOB=2S△PAB和S梯形AOBP+S梯形PMNB-S△AOB=2S△PAB,列出等式是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$,$\sqrt{3}$,$\sqrt{5}$ | B. | 3,4,5 | C. | 5,7,8 | D. | 6,8,10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
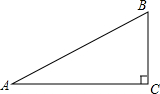 如图,在Rt△ACB中,∠ACB=90°
如图,在Rt△ACB中,∠ACB=90°查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com