
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 -3是$\sqrt{81}$=9的平方根;2<$\sqrt{5}$<3,整数部分是2.若a是一个无理数,且ab+a-b=1,可利用特殊值法得b=-1,同一平面内的三条直线两两相交,其交点个数为3或1个.关于y轴的对称点的坐标特点:横坐标互为相反数,纵坐标不变可得P(x,y)关于y轴的对称点P′的坐标为(-x,y).
解答 解::①-3是$\sqrt{81}$的平方根,说法正确;
②若$\sqrt{5}$的整数部分是a,则a=3,说法错误;
③若a是一个无理数,且ab+a-b=1,则b=-1,说法正确;
④同一平面内的三条直线两两相交,其交点个数为3,说法错误;
⑤平面直角坐标系内的一点P(x,y)关于y轴的对称点P′的坐标为(-x,y),说法正确;
正确的说法有3个,
故选:C.
点评 此题主要考查了关于y轴的对称点的坐标特点、平方根、相交线以及无理数,关键是掌握点的坐标的变化规律,以及 一个正数有两个平方根,这两个平方根互为相反数.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图1,矩形ABCD,AB=3,BC=4,E,F分别在AB,BC边上,且EF∥AC;将△BEF沿EF折叠,得△B'EF,设BE=x.
如图1,矩形ABCD,AB=3,BC=4,E,F分别在AB,BC边上,且EF∥AC;将△BEF沿EF折叠,得△B'EF,设BE=x.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
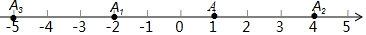 如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次点A向左移动3个单位长度到达点A1,第2次从点A1向右移动6个单位长度到达点A2,第3次从点A2向左移动9个单位长度到达点A3,…,按照这种移动规律进行下去,第n次移动到达点An,如果点An与原点的距离不小于50,那么n的最小值是33.
如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次点A向左移动3个单位长度到达点A1,第2次从点A1向右移动6个单位长度到达点A2,第3次从点A2向左移动9个单位长度到达点A3,…,按照这种移动规律进行下去,第n次移动到达点An,如果点An与原点的距离不小于50,那么n的最小值是33.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com