练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

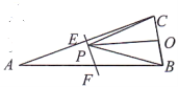
    【题目】如图，点O为等腰三角形ABC底边BC的中点,,,腰AC的垂直平分线EF分别交AB、AC于E、F点,若点P为线段EF上一动点，则△OPC周长的最小值为_________．

    【答案】27．

    【解析】

    连接AO，由于△ABC是等腰三角形，点O是BC边的中点，故AO⊥BC，再根据勾股定理求出AO的长，再再根据EF是线段AC的垂直平分线可知，点C关于直线EF的对称点为点A，故AO的长为CP+PO的最小值，由此即可得出结论．

    连接AO，


    ∵△ABC是等腰三角形，点O是BC边的中点，
    ∴AO⊥BC，

    ∴，

    ∵EF是线段AC的垂直平分线，
    ∴点C关于直线EF的对称点为点A，
    ∴AO的长为CP+PO的最小值，

    ∴△OPC周长的最小值．

    故答案为：27．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

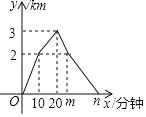
    【题目】小明和爸爸周末到湿地公园进行锻炼，两人同时从家出发，匀速骑共享单车到达公园入口，然后一同匀速步行到达驿站，到达驿站后小明的爸爸立即又骑共享单车按照来时骑行速度原路返回，在公园入口处改为步行，并按来时步行速度原路回家，小明到达驿站后逗留了10分钟之后骑车回家，爸爸在锻炼过程中离出发地的路程与出发的时间的函数关系如图．

    (1)图中m＝_____，n＝_____；(直接写出结果)

    (2)小明若要在爸爸到家之前赶上，问小明回家骑行速度至少是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某超市每天都用360元从批发商城批发甲乙两种型号“垃圾分类”垃圾桶进行零售,批发价和零售价如下表所示:

    批发价(元个)

    零售价(元/个)

    甲型号垃圾桶

    12

    16

    乙型号垃圾桶

    30

    36

    若设该超市每天批发甲型号“垃圾分类”垃圾桶x个,乙型号“垃圾分类”垃圾桶y个,

    （1）求y关于x的函数表达式.

    （2）若某天该超市老板想将两种型号的“垃圾分类”垃圾桶全部售完后,所获利润率不低于30%,则该超市至少批发甲型号“垃圾分类”垃圾桶多少个?(利润率=利润/成本).

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知:如图，BD为△ABC的角平分线，且BD=BC，E为BD延长线上的一点，BE=BA，过E作EF⊥AB，F为垂足，下列结论:①△ABD≌△EBC；②∠BCE+∠BCD=180°；③AD=EF=EC；④AE=EC，其中正确的是________(填序号)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，是内的一点.

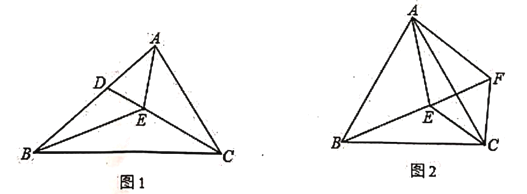
    （1）如图，平分交于点，点在线段上（点不与点、重合），且，求证：.

    （2）如图，若是等边三角形，，，以为边作等边，连.当是等腰三角形时，试求出的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】求证：等腰三角形两腰上的中线相等.

    （1）请用尺规作出△ABC两腰上的中线BD、CE（保留痕迹，不写作法）；

    （2）结合图形，写出已知、求证和证明过程.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，Q为正方形ABCD的CD边上一点，CQ=1，DQ=2，P为BC上一点，若PQ⊥AQ，则CP=_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,已知:在四边形ABFC中，=90的垂直平分线EF交BC于点D,交AB于点E,且CF=AE

    （1）试探究,四边形BECF是什么特殊的四边形;

    （2）当的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.

    (特别提醒:表示角最好用数字)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=ax2+bx+c的图象如图所示，有下列5个结论，①abc＜0； ②2a+b=0；③b2﹣4ac＜0；④a+b+c＞0；⑤a﹣b+c＜0．其中正确的结论有________（填序号）

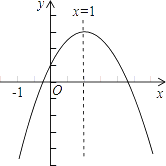
    查看答案和解析>>

    同步练习册答案