练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．三角形的两边长分别为8和6，第三边长是一元一次不等式2x-1＜9的正整数解，则三角形的第三边长是3或4．

    分析 先求出不等式的解集，再根据x是符合条件的正整数判断出x的可能值，再由三角形的三边关系求出x的值即可．

    解答 解：2x-1＜9，
    解得：x＜5，
    ∵x是它的正整数解，
    ∴x可取1，2，3，4，
    根据三角形第三边的取值范围，得2＜x＜14，
    ∴x=3，4．
    故答案为：3或4．

    点评 本题综合考查了求不等式特殊解的方法及三角形的三边关系，正确解不等式，求出解集是解答本题的关键．解不等式应根据不等式的基本性质．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2016-2017学年四川达县万家中学下学期九年级第一次月考数学试卷（解析版） 题型：选择题

    函数y＝和y＝在第一象限内的图象如图，点P是y＝的图象上一动点，PC⊥x轴于点C，交y＝的图象于点A. PD⊥y轴于点D，交y＝的图象于点B。.下面结论：①△ODB与△OCA的面积相等；②PA与PB始终相等；③四边形PAOB的面积大小不会发生变化；④CA=AP. 其中正确结论是

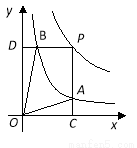
    A．①②③B．①②④ C．①③④D．②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图，在等边△ABC内有一点P，且PA=2，PB=$\sqrt{3}$，PC=1．
    （1）画出△PBC绕点B逆时针旋转60°后的图形（保留作图痕迹，不写画法）；
    （2）求∠BPC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图，已知△ABC．
    （1）实践与操作：
    利用尺规按下列要求作图，并在图中标明相应的字母（保留作图痕迹，不写作法）
    ①作BC边上的高AD；
    ②作△ABC的角平分线BE； 
    （2）综合与运用；
    若△ABC中，AB=AC且∠CAB=36°，
    请根据作图和已知写出符合括号内要求的正确结论；
    结论1：∠ABE=∠CBE=∠CAB=36°，∠BAD=∠CAD；（关于角）
    结论2：BD=DC，AE=BE，BC=BE；（关于线段）
    结论3：△ABE，△BCE都是等腰三角形．（关于三角形）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．甲、乙、丙三个人打乒乓球，为了确定哪两个人先打，商定三人伸出手来，若其中两人的手心或手背同时向上，则这两人先打，如果三个人手心或手背都向上则重来，则甲乙两先打的概率为（　　）
    A．$\frac{1}{2}$B．$\frac{1}{3}$C．$\frac{1}{4}$D．$\frac{1}{5}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．如图所示的三角形数垒，a、b是某行的前两个数，当a=7时，b=（　　）
    A．20B．21C．22D．23

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．如图，AB∥CD，点E在BC上，CD=CE，若∠ABC=34°，则∠D的度数是73°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，开口向下的抛物线y=ax2+bx+c交x轴于A（-1，0）、B（5，0）两点，交y轴于点C（0，5）
    （1）求抛物线的解析式；
    （2）设抛物线的顶点为D，求△BCD的面积；
    （3）在（2）的条件下，P、Q为线段BC上两点（P左Q右，且P、Q不与B、C重合），PQ=2$\sqrt{2}$，在第一象限的抛物线上是否存在这样的点R，使△PQR为等腰直角三角形？若存在，求出点R的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．圆锥底面圆的半径为3cm，其侧面展开图是半圆，则圆锥的母线长为（　　）
    A．3cmB．6cmC．9cmD．12cm

    查看答案和解析>>

    同步练习册答案