
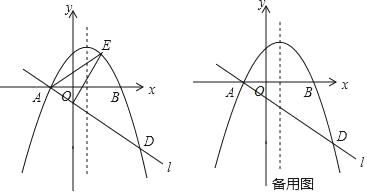
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������y=ax2��2ax��3a��a��0����x�ύ��A��B���㣨��A�ڵ�B����ࣩ��������A��ֱ��l��y=kx+b��y�Ḻ���ύ�ڵ�C���������ߵ���һ������ΪD����CD=4AC��
��1�������A������͵�D�ĺ����ꣻ
��2����E��ֱ��l�Ϸ����������ϵĶ��㣬����ACE����������ֵΪ![]() ����a��ֵ��
����a��ֵ��
��3����P�������ߵĶԳ����ϵ�һ�㣬��Q���������ϣ��Ե�A��D��P��QΪ������ı����ܷ��Ϊ���Σ����ܣ�ֱ��д����P�����ꣻ�����ܣ���˵�����ɣ�
���𰸡���1��A����1��0������D�ĺ�����Ϊ4����2��a=��![]() ����3����P��1����
����3����P��1����![]() ����1����4����
����1����4����
��������
��1���ⷽ�̼��ɵõ����ۣ�����ֱ��l��y=kx+b��A����1��0�����õ�ֱ��l��y=kx+k��
�ⷽ�̵õ���D�ĺ�����Ϊ4�����k=a���õ�ֱ��l�ĺ�������ʽΪy=ax+a��
��2����E��EF��y�ύֱ��l��F����E��x��ax2��2ax��3a�����õ�F��x��ax+a�������
EF=ax2��3ax��4a�����������ε������ʽ�з��̼��ɵõ����ۣ�
��3����ax2��2ax��3a=ax+a����ax2��3ax��4a=0���õ�D��4��5a������P��1��m��������AD
�Ǿ���ADPQ��һ���ߣ�����AD�Ǿ���APDQ�ĶԽ��ߣ��з��̼��ɵõ����ۣ�
�⣺��1����y=0ʱ��ax2��2ax��3a=0��
��ã�x1=��1��x2=3��
��A����1��0����B��3��0����
��ֱ��l��y=kx+b��A����1��0����
��0=��k+b��
��k=b��
��ֱ��l��y=kx+k��
����������ֱ��l���ڵ�A��D��
��ax2��2ax��3a=kx+k��
��ax2����2a+k��x��3a��k=0��
��CD=4AC��
���D�ĺ�����Ϊ4��
��2���ɣ�1��֪����D�ĺ�����Ϊ4��
![]()
��k=a��
��ֱ��l�ĺ�������ʽΪy=ax+a��
��E��EF��y�ύֱ��l��F����E��x��ax2��2ax��3a����
��F��x��ax+a����EF=ax2��2ax��3a��ax��a=ax2��3ax��4a��
��S��ACE=S��AFE��S��CEF![]() ��
��
![]()
���ACE����������ֵ=![]() ��
��
�ߡ�ACE����������ֵΪ![]() ��
��
��![]()
���![]()
��3���Ե�A��D��P��QΪ������ı����ܳ�Ϊ���Σ�
��ax2��2ax��3a=ax+a����ax2��3ax��4a=0��
��ã�x1=��1��x2=4��
��D��4��5a����
�������ߵĶԳ���Ϊֱ��x=1��
��P��1��m����
����AD�Ǿ���ADPQ��һ���ߣ�
����Q����4��21a����
m=21a+5a=26a����P��1��26a����
���ı���ADPQ�Ǿ��Σ�
���ADP=90�㣬
��AD2+PD2=AP2��
��52+��5a��2+32+��26a��5a��2=22+��26a��2��
��![]()
��a��0��
��![]()
��![]()
����AD�Ǿ���APDQ�ĶԽ��ߣ�
����Q��2����3a����
m=5a������3a��=8a����P��1��8a����
���ı���APDQ�Ǿ��Σ�
���APD=90�㣬
��AP2+PD2=AD2��
������1��1��2+��8a��2+��1��4��2+��8a��5a��2=52+��5a��2��
��![]()
��a��0��
��![]()
��P��1����4����
������������A��D��P��QΪ������ı����ܳ�Ϊ���Σ���![]() ��1����4����
��1����4����


 ��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ÿ�����Ľ���ʱ�ڣ���������������������ķ�ʽ��������һ����������������������Ƥ�����������������ȣ�������������ţ�Ϊ�˽����������������������ͬ�����ij����С����������˲��������ʾ��������ͼ��ʾ���������ݵ����������������в�������ͳ��ͼ��
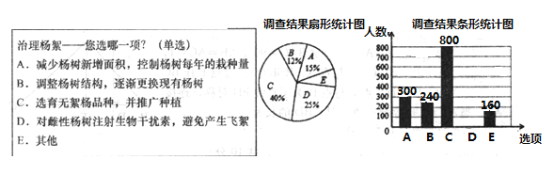
��������ͳ��ͼ������������⣺
��1�����ν��ܵ����������__________�ˣ�
��2���벹ȫ����ͳ��ͼ��
��3������ͳ��ͼ�����������![]() ��Բ�ĽǶ�����
��Բ�ĽǶ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
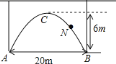
����Ŀ��һ������������������������ͼ������![]() �����
�����![]() ��
��
![]() �����ʵ���ֱ������ϵ�����������������߹�ϵʽ��
�����ʵ���ֱ������ϵ�����������������߹�ϵʽ��
![]() ���������µ�ƽ����˫���г��������м���һ����
���������µ�ƽ����˫���г��������м���һ����![]() �ĸ�����������е�һ���г����ܷ�����ʻ��
�ĸ�����������е�һ���г����ܷ�����ʻ��![]() ����
����![]() ������������������ļ�����Բ��ƣ�����˵˵������ɣ�
������������������ļ�����Բ��ƣ�����˵˵������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������IJ�����װ����״��С����ͬ������С��ÿ��С���ϸ�����һ�����֣��ֱ���1��2��3���ֹ涨�Ӳ�������ȡһ��С��Ӧ��������Ϊһ����λ����ʮλ���֣�Ȼ���С��Żش��в����ȣ����ŴӴ�������ȡһ��С��Ӧ��������Ϊ�����λ���ĸ�λ���֣�
��1�������û���״ͼ���б���������д���������涨�õ����п��ܵ���λ����
��2������Щ��λ������ȡһ������������ƽ��������4��С��5�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ��Ϊһ��ƽ����Ա�����֧��Ч��ͼ��AM�̶���ƽ����Ա��棬��ɻ��MB��CB�������֧����ƽ����Ե��¶�N�����ڱ�����CB���������ǹսǴ��Ļ��ȼ�ƽ����Ժͱ����ĺ�ȣ����Ƴ�ͼ��������AN��ʾƽ����ԣ�MΪAN�ϵĶ��㣬AN��CB��20 cm��AM��8 cm��MB��MN�����ǰ���ANB������б����
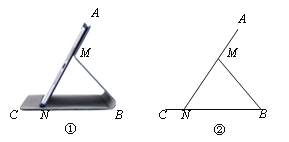
��1������б��Ϊ45��ʱ����CN�ij���
��2�������Ҫ����б����С��30������˵��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijС��������Ƶ�ʹ��Ƹ������������У�ͳ����ij�ֽ�����ֵ�Ƶ�ʣ���������ͼ��ʾ������ͼ����ô������һ������������п��ܵ��ǣ�������
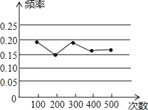
A. ��װ��1�������2��������ɫ����ȫ��ͬ���IJ����������������һ��������������
B. ��һ���˿����������ȡһ�ţ�������������ɫ����
C. ��һö�ʵؾ��ȵ�Ӳ�ң����ʱ����������泯����
D. ��һ���ʵؾ��ȵ������������ӣ����ʱ�泯�ϵĵ�����6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѧ���ϣ���ʦ����������⣺

С�ͬѧ���������£�

��ʦ˵����С骵�������ȷ����
��ش�С骵���ͼ������______________________________________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
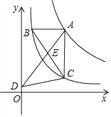
����Ŀ����ͼ����A�Ƿ���������y=![]() ͼ���ϵ�����һ�㣬����A��AB��x�ᣬAC��y�ᣬ�ֱ���������y=
ͼ���ϵ�����һ�㣬����A��AB��x�ᣬAC��y�ᣬ�ֱ���������y=![]() ��ͼ���ڵ�B��C������BC��E��BC��һ�㣬���Ӳ��ӳ�AE��y���ڵ�D������CD����S��DEC��S��BEA=_________��
��ͼ���ڵ�B��C������BC��E��BC��һ�㣬���Ӳ��ӳ�AE��y���ڵ�D������CD����S��DEC��S��BEA=_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��ͬѧ��ѧϰ��ȫ�������ε����֪ʶ���֣�ֻ��������ȫ��ͬ�ij�����ֱ�߾Ϳ�������һ���ǵ�ƽ���ߣ���ͼ��һ��ֱ��ѹס����OB����һ��ֱ��ѹס����OA�������һ��ֱ�߽��ڵ�P��С��˵��������OP���ǡ�BOA�Ľ�ƽ���ߣ�������������������(����)

A. �ǵ��ڲ����ǵ����ߵľ�����ȵĵ��ڽǵ�ƽ������
B. ��ƽ�����ϵĵ㵽��������ߵľ������
C. ������������ƽ���ߵĽ��㵽�����ߵľ������
D. ���Ͼ�����ȷ
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com