
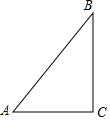
 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,若以C为圆心,r为半径画⊙C,请根据下列条件,求半径r的值或取值范围.
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,若以C为圆心,r为半径画⊙C,请根据下列条件,求半径r的值或取值范围.分析 (1)过点C作CD⊥AB于点D,再分圆与AB相切时;点A在圆内部,点B在圆上或圆外时,根据勾股定理以及直角三角形的面积计算出其斜边上的高,再根据位置关系与数量之间的联系进行求解;
(2)要使圆与斜边AB有两个交点,则应满足直线和圆相交,且半径不大于AC.要保证相交,只需求得相切时,圆心到斜边的距离,即斜边上的高即可;
(3)根据⊙C与斜边AB没有公共交点可知r<CD或点B在⊙C的内部,据此可得出结论.
解答 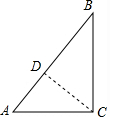 解:(1)如图,∵∠C=90°,AC=3,BC=4,
解:(1)如图,∵∠C=90°,AC=3,BC=4,
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴CD=$\frac{3×4}{5}$=2.4.
当圆与AB相切时,即r=CD=2.4;
当点A在圆内部,点B在圆上或圆外时,此时AC<r≤BC,即3<r≤4.
∴3<r≤4或r=2.4;
(2)∵BC>AC,
∴以C为圆心,R为半径所作的圆与斜边AB有两个交点,则圆的半径应大于CD,小于或等于AC,
∴r的取值范围是2.4<R≤3;
(3)∵⊙C与斜边AB没有公共交点,
∴r<CD或点B在⊙C的内部,
∴r<2.4或r>4.
点评 本题考查了对点与圆的位置关系的判断.关键要记住若半径为r,点到圆心的距离为d,则有:当d>r时,点在圆外;当d=r时,点在圆上,当d<r时,点在圆内.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
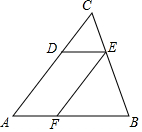 如图,点D、E、F分别是△ABC的边AC、BC、AB上的点,且有$\frac{CE}{CB}$=$\frac{CD}{CA}$=$\frac{1}{3}$,$\frac{BF}{BA}$=$\frac{BE}{BC}$=$\frac{2}{3}$,当△ABC的面积为18cm2时,求四边形AFED的面积.
如图,点D、E、F分别是△ABC的边AC、BC、AB上的点,且有$\frac{CE}{CB}$=$\frac{CD}{CA}$=$\frac{1}{3}$,$\frac{BF}{BA}$=$\frac{BE}{BC}$=$\frac{2}{3}$,当△ABC的面积为18cm2时,求四边形AFED的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,将矩形ABCD绕点B按顺时针方向旋转一个角α(0°<α<180°),得矩形BEFG,直线BG,EF交直线CD于点P,H.找出与BP相等的线段,并给出证明.
已知:如图,将矩形ABCD绕点B按顺时针方向旋转一个角α(0°<α<180°),得矩形BEFG,直线BG,EF交直线CD于点P,H.找出与BP相等的线段,并给出证明.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com