【题目】下列说法正确的是（ ）
A. 为了解苏州市中学生的睡眠情况，应该采用普查的方式
B. 某种彩票的中奖机会是
，则买
张这种彩票一定会中奖
C. 一组数据
，
，
，
，，
，
的众数和中位数都是
D. 若甲组数据的方差
，乙组数据的方差
，则乙组数据比甲组数据稳定
科目：初中数学 来源： 题型：
【题目】如图，点G，D，C在直线a上，点E，F，A，B在直线b上，若a∥b，Rt△GEF从如图所示的位置出发，沿直线b向右匀速运动，直到EG与BC重合．运动过程中△GEF与矩形ABCD重合部分的面积（S）随时间（t）变化的图象大致是（ ）
A. 
B. 
C. 
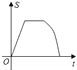D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知某种产品的进价为每件40元，现在的售价为每件60元，每星期可卖出300件．市场调查发现，该产品每降价1元，每星期可多卖出20件，由于供货方的原因销量不得超过380件，设这种产品每件降价x元（x为整数），每星期的销售利润为w元．
（1）求w与x之间的函数关系式，并写出自变量x的取值范围；
（2）该产品销售价定为每件多少元时，每星期的销售利润最大？最大利润是多少元？
（3）该产品销售价在什么范围时，每星期的销售利润不低于6000元，请直接写出结果．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商店从厂家以21元的价格购进一批商品，该商品可以自行定价，若每件商品售价为
元，则可卖出（350－10）件，但物价局限定每件商品加价不能超过进价的20%，商店计划要赚400元，需要卖出多少件商品?每件商品应售多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
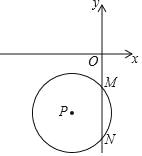
【题目】如图，半径为5的⊙P与y轴交于点M（0，﹣4），N（0，﹣10）
（1）求点P的坐标；
（2）将⊙P绕点O顺时针方向旋转90°后得⊙A，交x轴于B、C，求过A、B、C三个点的抛物线的解析式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，过y轴上一个动点M作x轴的平行线，交双曲线y=
于点A，交双曲线
于点B，点C、点D在x轴上运动，且始终保持DC＝AB，则平行四边形ABCD的面积是（ ）
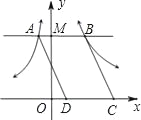
A. 7 B. 10 C. 14 D. 28
查看答案和解析>>
科目：初中数学 来源： 题型：
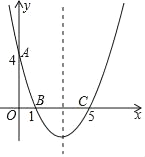
【题目】如图，在直角坐标系中，抛物线经过点A（0，4），B（1，0），C（5，0）
（1）求抛物线的解析式和对称轴；
（2）在抛物线的对称轴上是否存在一点P，使△PAB的周长最小？若存在，请求出点P的坐标；若不存在，请说明理由；
（3）该抛物线有一点D（x，y），使得S△ABC＝S△DBC，求点D的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC内接于⊙O，CA=CB，CD∥AB且与OA的延长线交与点D．
(1)判断CD与⊙O的位置关系并说明理由；
(2)若∠ACB=120°，OA=2，求CD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，A，B两点的坐标分别为A（2，2），B（2，﹣2）．对于给定的线段AB及点P，Q，给出如下定义：若点Q关于AB所在直线的对称点Q′落在△ABP的内部（不含边界），则称点Q是点P关于线段AB的内称点．
（1）已知点P（4，﹣1）．
①在Q1（1，﹣1），Q2（1，1）两点中，是点P关于线段AB的内称点的是 ；
②若点M在直线y＝x﹣1上，且点M是点P关于线段AB的内称点，求点M的横坐标xM的取值范围；
（2）已知点C（3，3），⊙C的半径为r，点D（4，0），若点E是点D关于线段AB的内称点，且满足直线DE与⊙C相切，求半径r的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
