
【题目】阅读下列两则材料,回答问题,
材料一:定义直线y=ax+b与直线y=bx+a互为“互助直线”,例如,直线y=x+4与直y=4x+1互为“互助直线“
材料二:对于平面直角坐标系中的任意两点P1(x1,y1)、P2(x2,y2),P1、P2两点间的直角距离d(P1,P2)=|x1﹣x2|+|y1﹣y2|.例如:Q1(﹣3,1)、Q2(2,4)两点间的直角距离为d(Q1,Q2)=|﹣3﹣2|+|1﹣4|=8
设P0(x0,y0)为一个定点,Q(x,y)是直线y=ax+b上的动点,我们把d(P0,Q)的最小值叫做P0到直线y=ax+b的直角距离.
(1)计算S(﹣1,6),T(﹣2,3)两点间的直角距离d(S,T)= ,直线y=2x+3上的一点H(a,b)又是它的“互助直线”上的点,求点H的坐标.
(2)对于直线y=ax+b上的任意一点M(m,n),都有点N(3m,2m﹣3n)在它的“互助直线”上,试求点L(5,﹣![]() )到直线y=ax+b的直角距离.
)到直线y=ax+b的直角距离.
【答案】(1)4;(2)5.
【解析】
(1)根据题中所给出的两点的直角距离公式即可得出结论;求两条直线的交点即可求H点的坐标;
(2)先表示直线y=ax+b的“互助直线”,并将点M和N分别代入可得方程组,得:(3b+3a﹣2)m=﹣a﹣3b,对于任意一点M(m,n)等式均成立,求出a,b的值,再根据题意得出关于x的式子,再由绝对值的几何意义即可得出结论.
解:(1)∵S(﹣1,6)、T(﹣2,3)则S、T两点的直角距离为d(S,T)=|﹣1﹣(﹣2)|+|6﹣3|=4,
∴S(﹣1,6)、T(﹣2,3)两点间的直角距离d(S,T)=4.
直线y=2x+3的“互助直线”是y=3x+2,由题意知H是它们的交点,则有:
![]() ,解得,
,解得,![]() ,
,
∴点H的坐标为:H(1,5).
故答案为:4.
(2)∵点M(m,n)是直线y=ax+b上的任意一点,
∴am+b=n①,
∵点N(3m,2m﹣3n)是直线y=ax+b的“互助直线”上的一点,
即N(3m,2m﹣3n)在直线y=bx+a上
∴3bm+a=2m﹣3n②,
将①代入②得,
3bm+a=2m﹣3(am+b),
整理得:3bm+3am﹣2m=﹣a﹣3b,
∴(3b+3a﹣2)m=﹣a﹣3b,
∵对于任意一点M(m,n)等式均成立,
∴![]() ,
,
解得 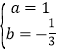 ,
,
∴y=x-![]() .
.
∵Q(x,y)是直线y=x-![]() 上的动点,定点L(5,﹣
上的动点,定点L(5,﹣![]() )
)
∴Q(x,x﹣![]() ),
),
∴d(L,Q)=|5﹣x|+|﹣![]() ﹣(x﹣
﹣(x﹣![]() )|=|5﹣x|+|﹣x|,
)|=|5﹣x|+|﹣x|,
∵当0≤x≤5时,代数式|5﹣x|+|﹣x|有最小值5,
∴点L(5,﹣![]() )到直线y=x-
)到直线y=x-![]() 的直角距离是5.
的直角距离是5.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】某条公共汽车线路收支差额![]() 与乘客量
与乘客量![]() 的函数关系如图所示(收支差额
的函数关系如图所示(收支差额![]() 车票收入
车票收入![]() 支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变支出费用,提高车票价格;建议(Ⅱ)不改变车票价格,减少支出费用. 下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )
支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变支出费用,提高车票价格;建议(Ⅱ)不改变车票价格,减少支出费用. 下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )

④ ③ ② ①
A. ①反映了建议(Ⅰ),③反映了建议(Ⅱ) B. ②反映了建议(Ⅰ),④反映了建议(Ⅱ)
C. ①反映了建议(Ⅱ),③反映了建议(Ⅰ) D. ②反映了建议(Ⅱ),④反映了建议(Ⅰ)
查看答案和解析>>
科目:初中数学 来源: 题型:
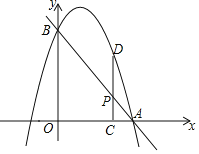
【题目】如图,已知直线![]() 分别交
分别交![]() 轴、
轴、![]() 轴于点A、B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC
轴于点A、B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC![]()
![]() 轴于点C,交抛物线于点D.
轴于点C,交抛物线于点D.
(1)若抛物线的解析式为![]() ,设其顶点为M,其对称轴交AB于点N.
,设其顶点为M,其对称轴交AB于点N.
①求点M、N的坐标;
②是否存在点P,使四边形MNPD为菱形?并说明理由;
(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形与![]() AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.
AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠A=90°,AB=AC,点D为BC的中点.
(1)如图①,若点E、F分别为AB、AC上的点,且DE⊥DF,求证:BE=AF;
(2)若点E、F分别为AB、CA延长线上的点,且DE⊥DF,那么BE=AF吗?请利用图②说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司推出一款新产品,通过市场调研后,按三种颜色受欢迎的程度分别对A颜色、B颜色、C颜色的产品在成本的基础上分别加价40%,50%,60%出售(三种颜色产品的成本一样),经过一个季度的经营后,发现C颜色产品的销量占总销量的40%,三种颜色产品的总利润率为51.5%,第二个季度,公司决定对A产品进行升级,升级后A产品的成本提高了25%,其销量提高了60%,利润率为原来的两倍;B产品的销量提高到与升级后的A产品的销量一样,C产品的销量比第一季度提高了50%,则第二个季度的总利润率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
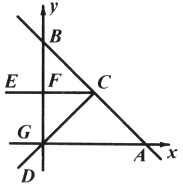
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是
是![]() 的中点,
的中点,![]() 绕点
绕点![]() 按顺时针旋转,且
按顺时针旋转,且![]() ,
,![]() 的一边
的一边![]() 交
交![]() 轴于点
轴于点![]() ,开始时另一边
,开始时另一边![]() 经过点
经过点![]() ,点
,点![]() 坐标为
坐标为![]() ,当
,当![]() 旋转过程中,射线
旋转过程中,射线![]() 与
与![]() 轴的交点由点
轴的交点由点![]() 到点
到点![]() 的过程中,则经过点
的过程中,则经过点![]() 三点的圆的圆心所经过的路径长为( )
三点的圆的圆心所经过的路径长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的布袋,甲袋中有两个完全相同的小球,分别标有数字1和-2;乙袋中有三个完全相同的小球,分别标有数字-1、0和2.小丽先从甲袋中随机取出一个小球,记录下小球上的数字为x;再从乙袋中随机取出一个小球,记录下小球上的数字为y,设点A的坐标为(x,y).
(1)请用表格或树状图列出点A所有可能的坐标;
(2)求点A在反比例函数y=![]() 图象上的概率.
图象上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com