
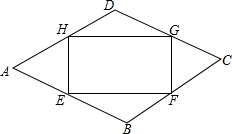
 某公园要在菱形场地ABCD内划出一个矩形活动场地EFGH,要求矩形的四个顶点E、F、G、H分别在菱形场地的四条边上,且BE=BF=DG=DH菱形的周长为4am,∠ADC=120°.
某公园要在菱形场地ABCD内划出一个矩形活动场地EFGH,要求矩形的四个顶点E、F、G、H分别在菱形场地的四条边上,且BE=BF=DG=DH菱形的周长为4am,∠ADC=120°.分析 (1)根据菱形的性质得△AHE是等边三角形,即HE=(1-x)米,过点P作DP⊥HG于点P,则HG=2HP=2DHsin∠HDP=$\sqrt{3}$x米,由矩形周长公式可得;
(2)根据矩形的面积公式即可得到结论;
(3)根据题意列方程即可得到结论.
解答 解:(1)∵四边形ABCD是菱形,
∴AB=AD=a米,
∵BE=BF=DH=DG=x米,
∵∠ADC=120°,∴∠A=60°,
∴AE=AH=(a-x)米,∠ADC=120°,
∴△AHE是等边三角形,即HE=(a-x)米,
如图,过点P作DP⊥HG于点P,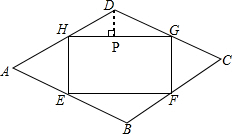
∴HG=2HP,∠HDP=$\frac{1}{2}$∠ADC=60°,
则HG=2HP=2DHsin∠HDP=2x×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$x米,
∴C=2(a-x+$\sqrt{3}$x)=(2$\sqrt{3}$-2)x+2a,(0<x<4);
(2)∵HE=(a-x)米,HG=$\sqrt{3}$x米,
∴S=$\sqrt{3}$x(a-x)=-$\sqrt{3}$x2+$\sqrt{3}$ax,(0<x<4),
当x=-$\frac{\sqrt{3}}{2(-\sqrt{3})}$a=$\frac{1}{2}$a时,
S最大=$\frac{-(\sqrt{3}a)^{2}}{4(-\sqrt{3})}$=$\frac{\sqrt{3}}{4}$a2;
(3)当矩形的面积为$\frac{\sqrt{3}{a}^{2}}{8}$m2,
即-$\sqrt{3}$x2+$\sqrt{3}$ax=$\frac{\sqrt{3}{a}^{2}}{8}$,
解得:x1=$\frac{2+\sqrt{2}}{4}$a,x2=$\frac{2-\sqrt{2}}{4}$a,
∴当BE=$\frac{2+\sqrt{2}}{4}$a,或$\frac{2-\sqrt{2}}{4}$am时,能获得需要的面积.
点评 题主要考查二次函数的实际应用,根据菱形的性质及等腰三角形性质、三角函数表示出矩形的长宽是求得函数解析式的前提,熟练掌握二次函数的性质是求函数最值的关键.


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直线1表示铁路,A、B两点表示某工厂两个生产区,若要在铁路旁修建一个货仓C,使货仓C到两个生产区A,B的距离之和最短,则这样的点C的位置( )
如图,直线1表示铁路,A、B两点表示某工厂两个生产区,若要在铁路旁修建一个货仓C,使货仓C到两个生产区A,B的距离之和最短,则这样的点C的位置( )| A. | 有1处 | B. | 有2处 | C. | 有4处 | D. | 不存在 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
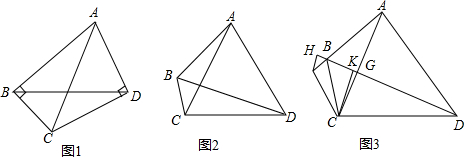
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
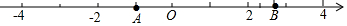
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com