
【题目】如图,某工程队从A点出发,沿北偏西67度方向修一条公路AD,在BD路段出现塌陷区,就改变方向,由B点沿北偏东23度的方向继续修建BC段,到达C点又改变方向,使所修路段CE∥AB,此时∠ECB有多少度?试说明理由.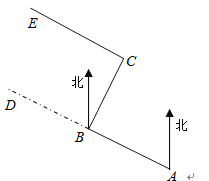
科目:初中数学 来源: 题型:
【题目】交通安全是社会关注的热点问题,安全隐患主要是超速和超载.某中学八年级数学活动小组的同学进行了测试汽车速度的实验.如图,先在笔直的公路1旁选取一点P,在公路1上确定点O、B,使得PO⊥l,PO=100米,∠PBO=45°.这时,一辆轿车在公路1上由B向A匀速驶来,测得此车从B处行驶到A处所用的时间为3秒,并测得∠APO=60°.此路段限速每小时80千米,试判断此车是否超速?请说明理由(参考数据: ![]() =1.41,
=1.41, ![]() =1.73).
=1.73). 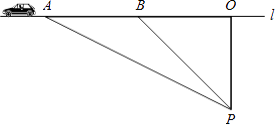
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2012四川雅安)在平面直角坐标系中,三角形ABC的三个顶点坐标分别是A(4,5),B(1,2),C(4,2),将三角形ABC向左平移5个单位后,A点的对应点A′的坐标是( )
A.(0,5)
B.(-1,5)
C.(9,5)
D.(-1,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校开展捐书活动,以下是5名同学捐书的册数:4,9,5,x,3,已知这组数据的平均数是5,则这组数据的中位数和众数分别是( )
A. 3和3 B. 4和4 C. 3和4 D. 5和5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填写下列解题过程中的推理根据:
已知:如图,点F、E分别在AB、CD上,AE、DF分别与BC相交于H、G,∠A=∠D,∠1+∠2=180°.说明:AB∥CD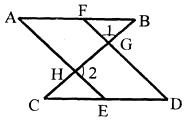
解:∵∠1=∠CGD()
∠1+∠2=180°
∴.
∴AE//FD ()
∴(两直线平行,同位角相等)
又∠A=∠D
∴∠D=∠BFD
∴()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与发现: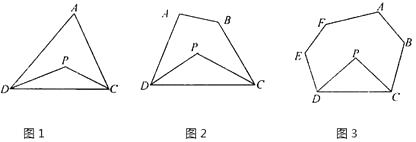
(1)探究一:三角形的一个内角与另两个内角的平分线所夹的角之间的关系
已知:如图1,在△ADC中,DP、CP分别平分∠ADC和∠ACD,
试探究∠P与∠A的数量关系,并说明理由.
(2)探究二:四边形的两个个内角与另两个内角的平分线所夹的角之间的关系
已知:如图2,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,
试探究∠P与∠A+∠B的数量关系,并说明理由.
(3)探究三:六边形的四个内角与另两个内角的平分线所夹的角之间的关系
已知:如图3,在六边形ABCDEF中,DP、CP分别平分∠EDC和∠BCD,
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com