
【题目】如图,点O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
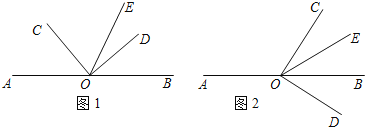
(1)如图(1),若∠AOC=![]() ,求∠DOE的度数;
,求∠DOE的度数;
(2)如图(2),将∠COD绕顶点O旋转,且保持射线OC在直线AB上方,在整个旋转过程中,当∠AOC的度数是多少时,∠COE=2∠DOB.
【答案】(1)20°;(2)综上所述,当∠AOC的度数是60°或108°时,∠COE=2∠DOB
【解析】
(1)依据邻补角的定义以及角平分线的定义,即可得到∠COE的度数,进而得出∠DOE的度数;
(2)设∠AOC=α,则∠BOC=180°-α,依据OE平分∠BOC,可得∠COE=![]() ×(180°-α)=90°-
×(180°-α)=90°-![]() α,再分两种情况,依据∠COE=2∠DOB,即可得到∠AOC的度数.
α,再分两种情况,依据∠COE=2∠DOB,即可得到∠AOC的度数.
(1)∵∠AOC=40°,
∴∠BOC=140°,
又∵OE平分∠BOC,
∴∠COE=![]() ×140°=70°,
×140°=70°,
∵∠COD=90°,
∴∠DOE=90°-70°=20°;
(2)设∠AOC=α,则∠BOC=180°-α,
∵OE平分∠BOC,
∴∠COE=![]() ×(180°-α)=90°-
×(180°-α)=90°-![]() α,
α,
分两种情况:
当OD在直线AB上方时,∠BOD=90°-α,

∵∠COE=2∠DOB,
∴90°-![]() α=2(90°-α),
α=2(90°-α),
解得α=60°.
当OD在直线AB下方时,∠BOD=90°-(180°-α)=α-90°,

∵∠COE=2∠DOB,
∴90°-![]() α=2(α-90°),
α=2(α-90°),
解得α=108°.
综上所述,当∠AOC的度数是60°或108°时,∠COE=2∠DOB.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
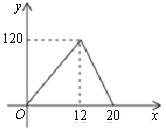
【题目】李刚家去年养殖的“丰收一号”多宝鱼喜获丰收,上市20天全部售完,李刚对销售情况进行了跟踪记录,并将记录情况绘成图象,日销售量y(单位:千克)与上市时间x(单位:天)的函数关系如图所示.
(1)观察图象,直接写出日销售量的最大值;
(2)求李刚家多宝鱼的日销售量y与上市时间x的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若点A在数轴上对应的数为a,点B在数轴上对应的数为b,且a,b满足|a+2|+(b﹣1)2=0.
![]()
(1)求线段AB的长;
(2)点C在数轴上对应的数为x,且x是方程2x﹣1=![]() x+2的解,在数轴上是否存在点P,使PA+PB=PC,若存在,直接写出点P对应的数;若不存在,说明理由;
x+2的解,在数轴上是否存在点P,使PA+PB=PC,若存在,直接写出点P对应的数;若不存在,说明理由;
(3)在(1)的条件下,将点B向右平移5个单位长度至点B’,此时在原点O处放一挡板,一小球甲从点A处以1个单位长度/秒的速度向左运动;同时另一小球乙从点B’处以2个单位长度/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),求甲、乙两小球到原点的距离相等时经历的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣3x+3与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线y= ![]() (k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y=
(k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y= ![]() (k≠0)上的点D1处,则a= .
(k≠0)上的点D1处,则a= . 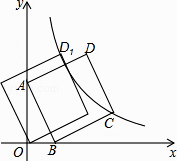
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC度数.
小明的解题思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠APC=50°+60°=110°.
问题迁移:
(1)如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.试判断∠CPD、∠α、∠β之间有何数量关系?请说明理由;


(2)在(1)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E. 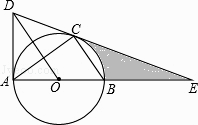
(1)求证:DE是⊙O的切线;
(2)若AE=6,CE=2 ![]() ,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π)
,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题12分)小明有5张写着不同数字的卡片,请按要求抽出卡片,完成下列各问题:
![]()
(1)从中取出2张卡片,使这2张卡片上数字的乘积最大,如何抽取?最大值是多少?
答:我抽取的2张卡片是 、 ,乘积的最大值为 .
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,如何抽取?最小值是多少?
答:我抽取的2张卡片是 、 ,商的最小值为 .
(3)从中取出4张卡片,用学过的运算方法,使结果为24.如何抽取?写出运算式子.(写出一种即可)
答:我抽取的4张卡片是 、 、 、 ,
算24的式子为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子里装着质地、大小都相同的3个红球和2个绿球,随机从中摸出一球,不再放回袋中,充分搅匀后再随机摸出一球.两次都摸到红球的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条南北方向的公路上,有一辆出租车停在A地,乘车的第一位客人向南走3千米下车;该车继续向南开,又走了2千米后,上来第二位客人,第二位客人乘车向北走7千米下车,此时恰好有第三位客人上车,先向北走3千米,又调头向南走,结果下车时出租车恰好到了A地.
(1)如果以A地为原点,向北方向为正方向,用1个单位表示1千米,在数轴上表示出第一位客人和第二位客人下车的位置;
(2)第三位客人乘车走了多少千米?
(3)规定出租车的收费标准是4千米内付7元,超过4千米的部分每千米加付1元(不足1千米按1千米算),那么该出租车司机在这三位客人中共收了多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com