
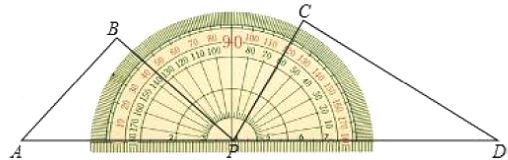
ЁОЬтФПЁПвЛИБШ§НЧГп(ЗжБ№КЌ45ЁуЃЌ45ЁуЃЌ90ЁуКЭ30ЁуЃЌ60ЁуЃЌ90Ёу)АДШчЭМЫљЪОАкЗХдкСПНЧЦїЩЯЃЌБпPDгыСПНЧЦї0ЁуПЬЖШЯпжиКЯЃЌБпAPгыСПНЧЦї180ЁуПЬЖШЯпжиКЯЃЌНЋШ§НЧГпABPШЦСПНЧЦїжааФЕуPвдУПУы10ЁуЕФЫйЖШЫГЪБеыа§зЊЃЌЕББпPBгы0ЁуПЬЖШЯпжиКЯЪБЭЃжЙдЫЖЏЃЌЩшШ§НЧГпABPЕФдЫЖЏЪБМфЮЊt.
ЃЈ1ЃЉЕБt=5ЪБЃЌБпPBОЙ§ЕФСПНЧЦїПЬЖШЯпЖдгІЕФЖШЪ§ЪЧ ЖШЃК
ЃЈ2ЃЉШєдкШ§НЧГпABPПЊЪМа§зЊЕФЭЌЪБЃЌШ§НЧГпPCDвВШЦЕуPвдУПУы2ЁуЕФЫйЖШФцЪБеыа§зЊЃЌЕБШ§НЧГпABPЭЃжЙа§зЊЪБЃЌШ§НЧГпPCDвВЭЃжЙа§зЊ.
ЂйЕБtЮЊКЮжЕЪБЃЌБпPBЦНЗжЁЯCPDЃЛ
Ђкдка§зЊЙ§ГЬжаЃЌЪЧЗёДцдкФГвЛЪБПЬЪЙЁЯBPD=2ЁЯAPCЃЌШєДцдкЃЌЧыжБНгаДГіtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉЂй
ЃЛЃЈ2ЃЉЂй![]() УыЃЛЂк
УыЃЛЂк![]() Уы
Уы
ЁОНтЮіЁП
ЃЈ1ЃЉИљОна§зЊЕФаджЪМДПЩМЦЫуЕУГіНсТлЃЛ
ЃЈ2ЃЉгЩа§зЊжЊЃЌ![]() ЕФа§зЊНЧЮЊ
ЕФа§зЊНЧЮЊ![]() ЃЌ
ЃЌ![]() ЕФа§зЊНЧЮЊ
ЕФа§зЊНЧЮЊ![]() ЃЌ
ЃЌ
ЂйИљОнPBЦНЗжЁЯCPDКЭЦННЧЕФЖЈвхСаГіЗНГЬМДПЩМЦЫуЕУГіЃЛ
ЂкЗжPAдкPCзѓВрКЭгвВрСНжжЧщПіБэЪОГі![]() ЃЌИљОнвбжЊНЈСЂЗНГЬМДПЩНтЕУНсТл.
ЃЌИљОнвбжЊНЈСЂЗНГЬМДПЩНтЕУНсТл.
ЃЈ1ЃЉЕБ![]() УыЪБЃЌ
УыЪБЃЌ![]() а§зЊСЫЃК
а§зЊСЫЃК![]()
Ёп![]() ЪЧЕШбќжБНЧШ§НЧаЮЃЌЁр
ЪЧЕШбќжБНЧШ§НЧаЮЃЌЁр![]() ЃЌ
ЃЌ
ДЫЪБЃЌБп![]() ОЙ§ЕФСПНЧЦїПЬЖШЯпЖдгІЕФЖШЪ§ЪЧЃК
ОЙ§ЕФСПНЧЦїПЬЖШЯпЖдгІЕФЖШЪ§ЪЧЃК![]() Лђ
Лђ![]()
ЁрБп![]() ОЙ§ЕФСПНЧЦїПЬЖШЯпЖдгІЕФЖШЪ§ЪЧЃК
ОЙ§ЕФСПНЧЦїПЬЖШЯпЖдгІЕФЖШЪ§ЪЧЃК![]()
ЃЈ2ЃЉЂйгЩа§зЊжЊЃЌ![]() ЕФа§зЊНЧЮЊ
ЕФа§зЊНЧЮЊ![]() ЃЌ
ЃЌ![]() ЕФа§зЊНЧЮЊ
ЕФа§зЊНЧЮЊ![]() ЃЌ
ЃЌ
ЁрБп![]() а§зЊЕФНЧЖШЮЊЃК
а§зЊЕФНЧЖШЮЊЃК![]() ЃЛБп
ЃЛБп![]() а§зЊЕФНЧЖШЮЊЃК
а§зЊЕФНЧЖШЮЊЃК![]() ЃЛ
ЃЛ
ЁрвРЬтвтЕУЃК![]() ЃЌМДЃК
ЃЌМДЃК![]()
Ёр![]() УыЃЛ
УыЃЛ
ЂкЕБPAдкPCзѓВрЪБЃЌгЩа§зЊжЊЃК
![]()
![]()
ИљОнЬтвтЃКЁЯBPD=2ЁЯAPCЃЌ
ЕУЃК![]() ЃЌМДЃК
ЃЌМДЃК![]()
Ёр![]() УыЃЛ
УыЃЛ
ЕБPAдкPCгвВрЪБЃЌгЩа§зЊжЊЃК
![]()
![]()
ИљОнЬтвтЃКЁЯBPD=2ЁЯAPCЃЌ
ЕУЃК![]() ЃЌМДЃК
ЃЌМДЃК![]()
Ёр![]() УыЃЛ
УыЃЛ
злЩЯЃК![]() УыЃЌЁЯBPD=2ЁЯAPC
УыЃЌЁЯBPD=2ЁЯAPC



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
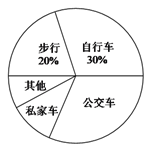
ЁОЬтФПЁПФГаЃЮЊСЫНтШЋаЃ2400УћбЇЩњЕНаЃЩЯбЇЕФЗНЪНЃЌдкШЋаЃЫцЛњГщШЁСЫШєИЩУћбЇЩњНјааЮЪОэЕїВщЃЎЮЪОэИјГіСЫЮхжжЩЯбЇЗНЪНЙЉбЇЩњбЁдёЃЌУПШЫжЛФмбЁвЛЯюЃЌЧвВЛФмВЛбЁЃЎНЋЕїВщЕУЕНЕФНсЙћЛцжЦГЩШчЭМЫљЪОЕФЦЕЪ§ЗжВМжБЗНЭМКЭЩШаЮЭГМЦЭМЃЈОљВЛЭъећЃЉЃЎ
ЃЈ1ЃЉетДЮЕїВщжаЃЌвЛЙВГщШЁСЫЖрЩйУћбЇЩњЃП
ЃЈ2ЃЉВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЛ
ЃЈ3ЃЉЙРМЦШЋаЃЫљгабЇЩњжагаЖрЩйШЫГЫзјЙЋНЛГЕЩЯбЇЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЦЫуЃКЃЈ1ЃЉЗжНтвђЪНЃКm2ЃЈxЉyЃЉ+4n2ЃЈyЉxЃЉЃЛ
ЃЈ2ЃЉНтВЛЕШЪНзщ![]() ЃЌВЂАбНтМЏдкЪ§жсЩЯБэЪОГіРДЃЛ
ЃЌВЂАбНтМЏдкЪ§жсЩЯБэЪОГіРДЃЛ
ЃЈ3ЃЉЯШЛЏМђЃЌдйЧѓНтЃЌ ![]() ЃЌЦфжаxЃН
ЃЌЦфжаxЃН![]() Љ2.
Љ2.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁУїбаОПЖўДЮКЏЪ§![]() ЃЈ
ЃЈ![]() ЮЊГЃЪ§ЃЉаджЪЪБгаШчЯТНсТлЃКЂйИУЖўДЮКЏЪ§ЭМЯѓЕФЖЅЕуЪМжедкЦНаагкxжсЕФжБЯпЩЯЃЛЂкИУЖўДЮКЏЪ§ЭМЯѓЕФЖЅЕугыxжсЕФСНИіНЛЕуЙЙГЩЕШбќжБНЧШ§НЧаЮЃЛЂлЕБ
ЮЊГЃЪ§ЃЉаджЪЪБгаШчЯТНсТлЃКЂйИУЖўДЮКЏЪ§ЭМЯѓЕФЖЅЕуЪМжедкЦНаагкxжсЕФжБЯпЩЯЃЛЂкИУЖўДЮКЏЪ§ЭМЯѓЕФЖЅЕугыxжсЕФСНИіНЛЕуЙЙГЩЕШбќжБНЧШ§НЧаЮЃЛЂлЕБ![]() ЪБЃЌyЫцxЕФдіДѓЖјдіДѓЃЌдђmЕФШЁжЕЗЖЮЇЮЊ
ЪБЃЌyЫцxЕФдіДѓЖјдіДѓЃЌдђmЕФШЁжЕЗЖЮЇЮЊ![]() ЃЛЂмЕу
ЃЛЂмЕу![]() гыЕу
гыЕу![]() дкКЏЪ§ЭМЯѓЩЯЃЌШє
дкКЏЪ§ЭМЯѓЩЯЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() .Цфжае§ШЗНсТлЕФИіЪ§ЮЊЃЈ ЃЉ
.Цфжае§ШЗНсТлЕФИіЪ§ЮЊЃЈ ЃЉ
A. 1B. 2C. 3D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГГЌЪаМЦЛЎЙКНјМзЁЂввСНжжаЭКХЕФНкФмЕЦЙВ1000жЛЃЌетСНжжНкФмЕЦЕФНјМлЁЂЪлМлШчЯТБэЃК
НјМлЃЈдЊ/жЛЃЉ | ЪлМлЃЈдЊ/жЛЃЉ | |
МзаЭ | 25 | 30 |
вваЭ | 45 | 60 |
ЃЈ1ЃЉШчЙћНјЛѕПюЧЁКУЮЊ37000дЊЃЌФЧУДПЩвдЙКНјМзаЭНкФмЕЦЖрЩйжЛЃП
ЃЈ2ЃЉГЌЪаЮЊЧьзЃдЊЕЉНјааДѓДйЯњЛюЖЏЃЌОіЖЈЖдвваЭНкФмЕЦНјааДђелЯњЪлЃЌвЊЧѓШЋВПЪлЭъКѓЃЌвваЭНкФмЕЦЕФРћШѓТЪЮЊ20%ЃЌЧыЮЪвваЭНкФмЕЦашДђМИелЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
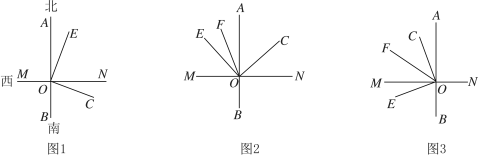
ЁОЬтФПЁПвбжЊЃК![]() ЮЊжБЯп
ЮЊжБЯп ![]() ЩЯЕФвЛЕуЃЌвд
ЩЯЕФвЛЕуЃЌвд![]() ЮЊЙлВьжааФЃЌЩфЯп
ЮЊЙлВьжааФЃЌЩфЯп![]() БэЪОе§ББЗНЯђЃЌ
БэЪОе§ББЗНЯђЃЌ![]() БэЪОе§ЖЋЗНЯђЃЈМД
БэЪОе§ЖЋЗНЯђЃЈМД![]() ЃЉЃЌЩфЯп
ЃЉЃЌЩфЯп![]() ЃЌЩфЯп
ЃЌЩфЯп![]() ЕФЗНЯђШчИїЭМЫљЪОЃЎ
ЕФЗНЯђШчИїЭМЫљЪОЃЎ
ЃЈ1ЃЉШчЭМ1ЫљЪОЃЌЕБ ![]() ЪБЃК
ЪБЃК
ЂйШє![]() ЃЌдђЩфЯп
ЃЌдђЩфЯп![]() ЕФЗНЯђЪЧ ЃЎ
ЕФЗНЯђЪЧ ЃЎ
Ђк ![]() гы
гы![]() ЕФЙиЯЕЮЊ ЃЌ
ЕФЙиЯЕЮЊ ЃЌ
Ђл ![]() гы
гы![]() ЕФЙиЯЕЮЊ ЃЎ
ЕФЙиЯЕЮЊ ЃЎ
ЃЈ2ЃЉШєНЋЩфЯп![]() ЃЌЩфЯп
ЃЌЩфЯп![]() ШЦЕу
ШЦЕу![]() а§зЊжСЭМ
а§зЊжСЭМ![]() ЕФЮЛжУЃЌСэвЛЬѕЩфЯп
ЕФЮЛжУЃЌСэвЛЬѕЩфЯп![]() ЧЁКУЦНЗж
ЧЁКУЦНЗж![]() ЃЌа§зЊжаЪМжеБЃГж
ЃЌа§зЊжаЪМжеБЃГж![]() ЃЎ
ЃЎ
ЂйШє![]() ЃЌдђ
ЃЌдђ![]() ЖШ .
ЖШ .
ЂкШє![]() ЃЌдђ
ЃЌдђ![]() ЃЈгУКЌ
ЃЈгУКЌ ![]() ЕФДњЪ§ЪНБэЪОЃЉЃЎ
ЕФДњЪ§ЪНБэЪОЃЉЃЎ
ЃЈ3ЃЉШєНЋЩфЯп![]() ЃЌЩфЯп
ЃЌЩфЯп![]() ШЦЕу
ШЦЕу![]() а§зЊжСЭМ
а§зЊжСЭМ![]() ЕФЮЛжУЃЌЩфЯп
ЕФЮЛжУЃЌЩфЯп![]() ШдШЛЦНЗж
ШдШЛЦНЗж![]() ЃЌа§зЊжаЪМжеБЃГж
ЃЌа§зЊжаЪМжеБЃГж![]() ЃЌдђ
ЃЌдђ![]() гы
гы![]() жЎМфДцдкдѕбљЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
жЎМфДцдкдѕбљЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
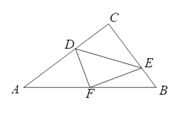
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯACB=90ЁуЃЌЕуD,EЗжБ№дкAC,BCЩЯЃЌЧвЁЯCDE=ЁЯBЃЌНЋЁїCDE биDEелЕўЃЌЕуCЧЁКУТфдкABБпЩЯЕФЕуFДІЃЌШєAC=8,AB=10ЃЌдђCDЕФГЄЮЊ____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкжБНЧзјБъЯЕжаЃЌвЛДЮКЏЪ§![]() ЕФЭМЯѓ
ЕФЭМЯѓ![]() гые§БШР§КЏЪ§ЕФЭМЯѓ
гые§БШР§КЏЪ§ЕФЭМЯѓ![]() НЛгкЕу
НЛгкЕу![]() ЃЌвЛДЮКЏЪ§
ЃЌвЛДЮКЏЪ§![]() ЕФЭМЯѓЮЊ
ЕФЭМЯѓЮЊ![]() ЃЌЧв
ЃЌЧв![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ФмЮЇГЩШ§НЧаЮЃЌдђдкЯТСаЫФИіЪ§жаЃЌ
ФмЮЇГЩШ§НЧаЮЃЌдђдкЯТСаЫФИіЪ§жаЃЌ![]() ЕФжЕФмШЁЕФЪЧЃЈЁЁЁЁЃЉ
ЕФжЕФмШЁЕФЪЧЃЈЁЁЁЁЃЉ
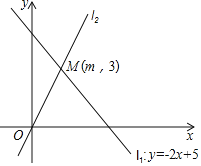
A. Љ2B. 1C. 2D. 3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕу![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЗжБ№ЪЧЫФБпаЮ
ЗжБ№ЪЧЫФБпаЮ![]() Бп
Бп![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЕФжаЕуЃЎдђЯТСаЫЕЗЈЃКЂйШє
ЕФжаЕуЃЎдђЯТСаЫЕЗЈЃКЂйШє![]() ЃЌдђЫФБпаЮ
ЃЌдђЫФБпаЮ![]() ЮЊОиаЮЃЛЂкШє
ЮЊОиаЮЃЛЂкШє![]() ЃЌдђЫФБпаЮ
ЃЌдђЫФБпаЮ![]() ЮЊСтаЮЃЛЂлШєЫФБпаЮ
ЮЊСтаЮЃЛЂлШєЫФБпаЮ![]() ЪЧЦНааЫФБпаЮЃЌдђ
ЪЧЦНааЫФБпаЮЃЌдђ![]() гы
гы![]() ЛЅЯрЦНЗжЃЛЂмШєЫФБпаЮ
ЛЅЯрЦНЗжЃЛЂмШєЫФБпаЮ![]() ЪЧе§ЗНаЮЃЌдђ
ЪЧе§ЗНаЮЃЌдђ![]() гы
гы![]() ЛЅЯрДЙжБЧвЯрЕШЃЎЦфжае§ШЗЕФИіЪ§ЪЧЃЈ ЃЉ
ЛЅЯрДЙжБЧвЯрЕШЃЎЦфжае§ШЗЕФИіЪ§ЪЧЃЈ ЃЉ
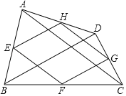
A. 1 B. 2 C. 3 D. 4
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com