

·ÖĪö £Ø1£©½ā·½³Ģx2-7x+12=0£¬¼“æÉĒó³öABÓėBCµÄ³¤£»
£Ø2£©ÓÉĢāŅāĮŠ³ö·½³Ģ${3^2}+{£Øt-3£©^2}=\sqrt{10}$£¬½ā·½³Ģ¼“æÉµĆ³ö½įĀŪ£»
£Ø3£©“ęŌŚµćP£¬Ź¹”÷ABPŹĒµČŃüČż½ĒŠĪ£¬ĄūÓƵČŃüČż½ĒŠĪµÄŠŌÖŹŗĶÖ±½ĒČż½ĒŠĪµÄŠŌÖŹ·ÖČżÖÖĒéæöĢÖĀŪ£¬Ēó³ötµÄÖµ¼“æÉ£®
½ā“š ½ā£ŗ£Ø1£©”ßx2-7x+12=£Øx-3£©£Øx-4£©=0£¬
”ąx1=3»ņx2=4£®
ŌņAB=3£¬BC=4£¬
£Ø2£©ÓÉĢāŅāµĆ${3^2}+{£Øt-3£©^2}=\sqrt{10}$£¬
”ąt1=4£¬t2=2£ØÉįČ„£©
Ōņt=4Ź±£¬AP=$\sqrt{10}$£¬
£Ø3£©“ęŌŚµćP£¬Ź¹”÷ABPŹĒµČŃüČż½ĒŠĪ£®
ŌŚRt”÷ABCÖŠ£¬AB=3£¬BC=4£¬øł¾Ż¹“¹É¶ØĄķµĆ£¬AC=5£¬
¢Łµ±AP=AB=3Ź±£¬ČēĶ¼1£¬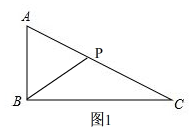 £¬
£¬
”ąPC=AC-AP=5-3=2£¬
”ąµćPŌĖ¶ÆĀ·³ĢŹĒAB+BC+PC=3+4+2=9£¬
”ąt=9£ØĆė£©£®
¢Śµ±BP=BA=3Ź±£¬ČēĶ¼2£¬
µ±PŌŚACÉĻŹ±£¬
¹żµćB×÷BD”ĶACÓŚD£¬
øł¾Ż”÷ABCµÄĆ껿µĆ£¬$\frac{1}{2}$BD•AC=$\frac{1}{2}$AB•BC£¬
”ąBD=$\frac{12}{5}$
ŌŚRt”÷ABDÖŠ£¬AB=3£¬BD=$\frac{12}{5}$£¬
øł¾Ż¹“¹É¶ØĄķµĆ£¬AD=$\frac{9}{5}$£¬
”ąPC=AC-2AD=$\frac{7}{5}$£¬
”ąµćPŌĖ¶ÆµÄĀ·³ĢĪŖAB+BC+PC=3+4+$\frac{7}{5}$=$\frac{42}{5}$£¬
”ąt=$\frac{42}{5}$£ØĆė£©
µ±PŌŚBCÉĻŹ±£¬ČēĶ¼3£¬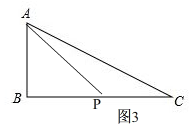 £¬
£¬
”ąµćPŌĖ¶ÆµÄĀ·³ĢĪŖAB+BP=3+3=6£¬
”ąt=6£ØĆė£©
¢Ūµ±BP=AP £Ø¼“PĪŖACÖŠµćŹ±£©£¬
”ąt=9.5£ØĆė£©
æÉÖŖµ±tĪŖ9Ćė»ņ9.5Ćė»ņ6£ØĆė£©»ņ$\frac{42}{5}$£ØĆė£©Ź±£¬”÷ABPŹĒµČŃüČż½ĒŠĪ£®
µćĘĄ “ĖĢāŹĒČż½ĒŠĪ×ŪŗĻĢā£¬Ö÷ŅŖæ¼²éĮĖÖ±½ĒČż½ĒŠĪµÄŠŌÖŹ£¬µČŃüČż½ĒŠĪµÄŠŌÖŹ£¬½āŅ»ŌŖ¶ž“Ī·½³ĢµÄ·½·Ø£¬½ā£Ø1£©µÄ¹Ų¼üŹĒÕĘĪÕŅ»ŌŖ¶ž“Ī·½³ĢµÄ½ā·Ø£¬½ā£Ø2£©µÄ¹Ų¼üŹĒ½ØĮ¢·½³ĢĒó½ā£¬½ā£Ø3£©µÄ¹Ų¼üŹĒ·ÖĄąĢÖĀŪ£®


 דŌŖ·»Č«³ĢĶ»Ęʵ¼Į·²āĻµĮŠ“š°ø
דŌŖ·»Č«³ĢĶ»Ęʵ¼Į·²āĻµĮŠ“š°ø Ö±ĶعóÖŻĆūŠ£ÖܲāŌĀæ¼Ö±ĶØĆūŠ£ĻµĮŠ“š°ø
Ö±ĶعóÖŻĆūŠ£ÖܲāŌĀæ¼Ö±ĶØĆūŠ£ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | Ö±½ĒČż½ĒŠĪ | B£® | µČ±ßČż½ĒŠĪ | C£® | µČŃüČż½ĒŠĪ | D£® | µČŃüÖ±½ĒČż½ĒŠĪ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | + | B£® | - | C£® | +»ņ”Į | D£® | -»ņ”Ā |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
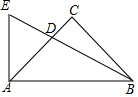 ČēĶ¼£¬”÷ABCÖŠ£¬”ĻC=90”ć£¬CA=CB£¬DĪŖACÉĻµÄŅ»µć£¬AD=2CD£¬AE”ĶAB½»BDµÄŃÓ³¤ĻßÓŚE£¬Ōņ$\frac{DE}{DB}$=$\frac{1}{2}$£®
ČēĶ¼£¬”÷ABCÖŠ£¬”ĻC=90”ć£¬CA=CB£¬DĪŖACÉĻµÄŅ»µć£¬AD=2CD£¬AE”ĶAB½»BDµÄŃÓ³¤ĻßÓŚE£¬Ōņ$\frac{DE}{DB}$=$\frac{1}{2}$£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
 ČēĶ¼£¬OP=1£¬¹żP×÷PP1”ĶOP£¬µĆOP1=$\sqrt{2}$£»ŌŁ¹żP1×÷P1P2”ĶOP1ĒŅP1P2=1£¬µĆOP2=$\sqrt{3}$£»ÓÖ¹żP2×÷P2P3”ĶOP2ĒŅP2P3=1£¬µĆOP3=2£»”ŅĄ“Ė·Ø¼ĢŠų×÷ĻĀČ„£¬Čō”÷OPnPn+1µÄĆ껿“óÓŚ6Ź±£¬nÖĮÉŁŹĒ144£®
ČēĶ¼£¬OP=1£¬¹żP×÷PP1”ĶOP£¬µĆOP1=$\sqrt{2}$£»ŌŁ¹żP1×÷P1P2”ĶOP1ĒŅP1P2=1£¬µĆOP2=$\sqrt{3}$£»ÓÖ¹żP2×÷P2P3”ĶOP2ĒŅP2P3=1£¬µĆOP3=2£»”ŅĄ“Ė·Ø¼ĢŠų×÷ĻĀČ„£¬Čō”÷OPnPn+1µÄĆ껿“óÓŚ6Ź±£¬nÖĮÉŁŹĒ144£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
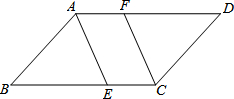 ČēĶ¼£¬ŅŃÖŖ?ABCDÖŠ£¬AEĘ½·Ö”ĻBAD£¬CFĘ½·Ö”ĻBCD£¬·Ö±š½»BC”¢ADÓŚE”¢F£®ĒóÖ¤£ŗDF=BE£®
ČēĶ¼£¬ŅŃÖŖ?ABCDÖŠ£¬AEĘ½·Ö”ĻBAD£¬CFĘ½·Ö”ĻBCD£¬·Ö±š½»BC”¢ADÓŚE”¢F£®ĒóÖ¤£ŗDF=BE£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
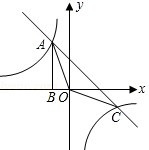 ČēĶ¼£¬Rt”÷ABOµÄ¶„µćAŹĒĖ«ĒśĻßy=$\frac{k}{x}$ÓėÖ±Ļßy=-x-£Øk+1£©ŌŚµŚ¶žĻóĻŽµÄ½»µć£¬AB”ĶxÖįÓŚµćBĒŅS”÷ABO=$\frac{3}{2}$£®
ČēĶ¼£¬Rt”÷ABOµÄ¶„µćAŹĒĖ«ĒśĻßy=$\frac{k}{x}$ÓėÖ±Ļßy=-x-£Øk+1£©ŌŚµŚ¶žĻóĻŽµÄ½»µć£¬AB”ĶxÖįÓŚµćBĒŅS”÷ABO=$\frac{3}{2}$£®²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com