
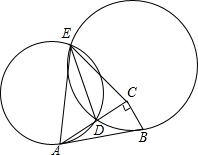
 给定直角三角形ABC,点D是AC边上任意一点.两个圆与直线AB分别相切于点A和B,这两个圆交于D和E两点.求证:∠BAC=∠DEC.
给定直角三角形ABC,点D是AC边上任意一点.两个圆与直线AB分别相切于点A和B,这两个圆交于D和E两点.求证:∠BAC=∠DEC. 分析 如图,延长ED交AB于F.根据切割线定理,得到FA2=FD•FE,FB2=FD•FE,推出AF=FB,推出,CF=AF=FB,再证明△CFD∽△EFC,由此即可解决问题.
解答 证明:如图,延长ED交AB于F.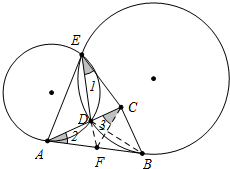
∵AB是两圆的公切线,
∴FA2=FD•FE,FB2=FD•FE,
∴AF2=FB2,
∴AF=FB,
∵∠ACB=90°,
∴CF=FA=FB,
∴∠1=∠3,
∴CF2=FD•FE,
∴$\frac{CF}{DF}$=$\frac{FE}{CF}$,∵∠DFC=∠CFE,
∴△CFD∽△EFC,
∴∠3=∠1,
∴∠1=∠2.
∴∠BAC=∠DEC.
点评 本题考查切线的性质、切线长定理,直角三角形斜边中线性质、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造相似三角形,题目比较难,用到切线定理.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
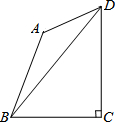 如图,四边形ABCD中,∠BAD=135°,∠BCD=90°,AB=BC=4,tan∠BDC=$\frac{\sqrt{6}}{3}$.
如图,四边形ABCD中,∠BAD=135°,∠BCD=90°,AB=BC=4,tan∠BDC=$\frac{\sqrt{6}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
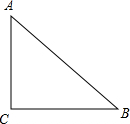 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,现有一点O从点A出发,沿AB方向运动,当到达点B时,运动停止,以点O为圆心,r为半径的圆记为⊙O.
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,现有一点O从点A出发,沿AB方向运动,当到达点B时,运动停止,以点O为圆心,r为半径的圆记为⊙O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com