
【题目】小文同学统计了某栋居民楼中全体居民每周使用手机支付的次数,并绘制了直方图.根据图中信息,下列说法错误的是( )
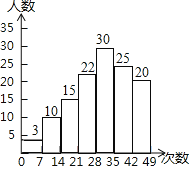
A.这栋居民楼共有居民125人
B.每周使用手机支付次数为28~35次的人数最多
C.有的人每周使用手机支付的次数在35~42次
D.每周使用手机支付不超过21次的有15人
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“作平行四边形的高”的尺规作图过程
已知:平行四边形ABCD.
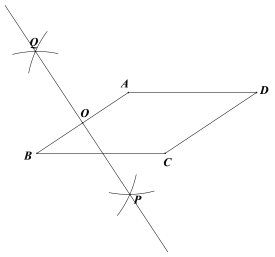
求作:![]() ,垂足为点E.
,垂足为点E.
作法:如图,
①分别以点A和点B为圆心,大于![]() 的长为半径作弧,两弧相交于P,Q两点;
的长为半径作弧,两弧相交于P,Q两点;
②作直线PQ,交AB于点O;
③以点O为圆心,OA长为半径做圆,交线段BC于点E;
④连接AE.
所以线段AE就是所求作的高.
根据小明设计的尺规作图过程
⑴使用直尺和圆规,补全图形;(保留作图痕迹)
⑵完成下面的证明
证明:![]() AP=BP, AQ= ,
AP=BP, AQ= ,
![]() PQ为线段AB的垂直平分线.
PQ为线段AB的垂直平分线.
![]() O为AB中点.
O为AB中点.
![]() AB为直径,⊙O与线段BC交于点E,
AB为直径,⊙O与线段BC交于点E,
![]()
![]()
![]() .( )(填推理的依据)
.( )(填推理的依据)
![]()
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
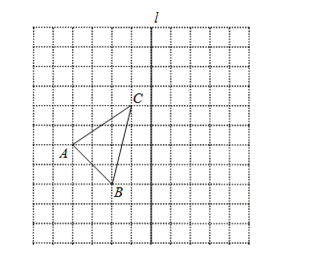
【题目】如图,在![]() 的正方形网格中,每个小正方形的边长都为1,网格中有一个格点
的正方形网格中,每个小正方形的边长都为1,网格中有一个格点![]() (即三角形的顶点都在格点上).
(即三角形的顶点都在格点上).
(1)在图中作出![]() 关于直线l对称的
关于直线l对称的![]() ;(要求A与
;(要求A与![]() ,B与
,B与![]() ,C与
,C与![]() 相对应)
相对应)
(2)作出![]() 绕点C顺时针方向旋转90°后得到的
绕点C顺时针方向旋转90°后得到的![]() ;
;
(3)在(2)的条件下求出线段CB在旋转中所扫过的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区教育系统为了更好地宣传扫黑除恶专项斗争,印制了应知应会手册,该区教育局想了解教师对扫黑除恶专项斗争应知应会知识掌握程度,抽取了部分教师进行了测试,并将测试成绩绘制成下面两幅统计图,请根据统计图中提供的信息,回答下面问题:
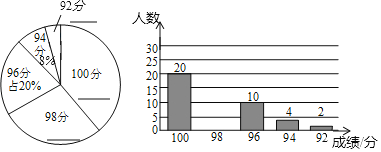
(1)计算样本中,成绩为98分的教师有 人,并补全两个统计图;
(2)样本中,测试成绩的众数是 ,中位数是 ;
(3)若该区共有教师6880名,根据此次成绩估计该区大约有多少名教师已全部掌握扫黑除恶专项斗争应知应会知识?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在城市改造中,市政府欲在一条人工河上架一座桥,河的两岸PQ与MN平行,河岸MN上有A、B两个相距50米的凉亭,小亮在河对岸D处测得∠ADP=60°,然后沿河岸走了110米到达C处,测得∠BCP=30°,求这条河的宽.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习完概率的有关内容后,小军与小波共同发明了一种利用“字母棋”进行比胜负的游戏,他们制作了5颗棋子,并在每颗棋子上标注相应的字母(棋子除了字母外,材质、大小、质地均相同),其中标有字母X的棋子有1颗,标有字母Y和Z的棋子分别有2颗.游戏规定:将5颗棋子放入一个不透明的袋子中,然后从5颗棋子中随机摸出两颗棋子,若摸到的两颗棋子标有字母X,则小军胜;若摸到两颗相同字母的棋子,则小波胜,其余情况为平局,则游戏重新进行.
(1)求随机摸到标有字母Y的棋子的概率;
(2)在游戏刚准备进行的同时,数学课代表小亮对游戏的公平性产生了质疑,请你通过列表法或者画树状图的方法帮小亮同学验证该游戏的规则是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2﹣2ax﹣2的图象(记为抛物线C1)顶点为M,直线l:y=2x﹣a与x轴,y轴分别交于A,B.
(1)对于抛物线C1,以下结论正确的是 ;
①对称轴是:直线x=1;②顶点坐标(1,﹣a﹣2);③抛物线一定经过两个定点.
(2)当a>0时,设△ABM的面积为S,求S与a的函数关系;
(3)将二次函数y=ax2﹣2ax﹣2的图象C1绕点P(t,﹣2)旋转180°得到二次函数的图象(记为抛物线C2),顶点为N.
①当﹣2≤x≤1时,旋转前后的两个二次函数y的值都会随x的增大而减小,求t的取值范围;
②当a=1时,点Q是抛物线C1上的一点,点Q在抛物线C2上的对应点为Q',试探究四边形QMQ'N能否为正方形?若能,求出t的值,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,内角A、B、C的对边分别为a、b、c.若b2+c2=2b+4c﹣5且a2=b2+c2﹣bc,则△ABC的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
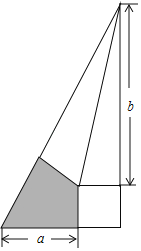
【题目】我国魏晋时期的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式,后人借助这种分割方法所得的图形证明了勾股定理.如图所示,若a=2,b=3,现随机向该图形内掷一枚小针,则针尖落在阴影域内的概率为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com