
【题目】某游泳馆的游泳池长50米,甲、乙二人分别在游泳池相对的A、B两边同时向另一边游去,其中s表示与A边的距离,t表示游泳时间,如图,l1 , l2分别表示甲、乙两人的s与t的关系.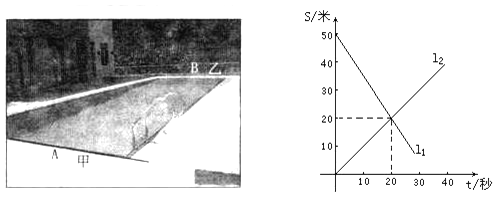
(1)l1表示谁到A边的距离s与游泳时间t的关系;
(2)甲、乙哪个速度快?
(3)游泳多长时间,两人相遇?
(4)t=30秒时,两人相距多少米?
【答案】
(1)解:由于当 ![]() 时,乙距离A为50米,所以l1表示谁到A边的距离s与游泳时间t的关系
时,乙距离A为50米,所以l1表示谁到A边的距离s与游泳时间t的关系
(2)解:由图象可知,到达终点时,乙所花时间比甲少,故乙比较快
(3)解:当两个人的函数图象相交时,即两个人相遇,此时为 ![]() s
s
(4)设l1表达式为 ![]() ,把
,把 ![]() ,
, ![]() ;
; ![]() ,
, ![]() 代入上式得
代入上式得 ![]() , k 1 =
, k 1 =![]() ,所以l1的表达式为
,所以l1的表达式为 ![]() ,当
,当 ![]() 时,
时, ![]() 。设l2表达式为
。设l2表达式为 ![]() ,把
,把 ![]() ,
, ![]() 代入上式,得
代入上式,得 ![]() ,所以l2的表达式为
,所以l2的表达式为 ![]() ,当
,当 ![]() ,
, ![]() ,两人相距
,两人相距 ![]() (米)
(米)
【解析】(1)当 t = 0 时,乙距离A为50米,所以l1表示乙到A边的距离s与游泳时间t的关系。
(2)由图象可知,到达终点时,乙所花时间比甲少,所以乙比较快。
(3)由图象可知, t = 20时,两个人相遇。
(4)设l1表达式为 s = k 1 t + b ,把 t = 20 , s = 20 ; t = 0 , s = 50 代入上式计算即可得到 b和 ![]() 的值,则l1的表达式可求,再将t = 30 代入l1的表达式可求 s的值;由题意设l2表达式为 s =
的值,则l1的表达式可求,再将t = 30 代入l1的表达式可求 s的值;由题意设l2表达式为 s = ![]() t,把 t = 20 , s = 20 代入上式,得
t,把 t = 20 , s = 20 代入上式,得 ![]() 的值,l2的表达式可求,再将t = 30 代入l2的表达式可求 s的值,两人相距 即为他们的距离之差。
的值,l2的表达式可求,再将t = 30 代入l2的表达式可求 s的值,两人相距 即为他们的距离之差。


 作业辅导系列答案
作业辅导系列答案科目:初中数学 来源: 题型:
【题目】如图1,等边三角形ABC中,点D在AB上(点D与点A,B不重合),DE⊥BC,垂足为E,点P在BC上,且DP∥AC,△B′DE′与△BDE关于DP对称.设BE=x,△B′DE′与△ABC重叠部分的面积为S,S关于x的函数图象如图2所示(其中0<x<![]() ,
, ![]() ≤x<m与m≤x<n时,函数的解析式不同).
≤x<m与m≤x<n时,函数的解析式不同).
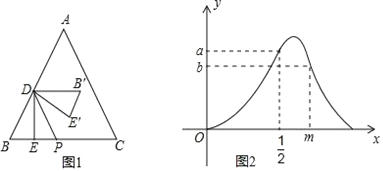
(1)填空:等边三角形ABC的边长为_____,图2中a的值为_____;
(2)求S关于x的函数关系式,并直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AD=8cm,AB=6cm.动点E从点C开始沿边CB向点B以2cm/s的速度运动,动点F从点C同时出发沿边CD向点D以1cm/s的速度运动至点D停止.如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是下图中的( )
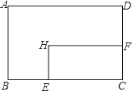
A. 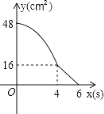 B.
B. 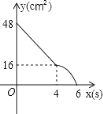 C.
C. 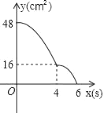 D.
D. 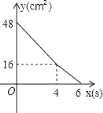
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标![]() 中,正比例函数
中,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象经过点
的图象经过点![]() .
.
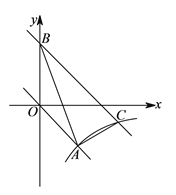
(![]() )分别求这两个函数的表达式.
)分别求这两个函数的表达式.
(![]() )将直线
)将直线![]() 向上平移
向上平移![]() 个单位长度后与
个单位长度后与![]() 轴交于点
轴交于点![]() ,与反比例函数图象在第四象限内的交点为
,与反比例函数图象在第四象限内的交点为![]() ,连接
,连接![]() 、
、![]() ,求点
,求点![]() 的坐标及
的坐标及![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A地将一批物品运往B地,再返回A地,图6表示两车离A地的距离s(千米)随时间t(小时)变化的图象,已知乙车到达B地后以30千米/小时的速度返回.请根据图象中的数据回答: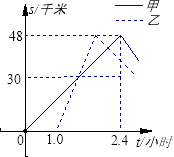
(1)甲车出发多长时间后被乙车追上?
(2)甲车与乙车在距离A地多远处迎面相遇?
(3)甲车从B地返回的速度多大时,才能比乙车先回到A地?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com