
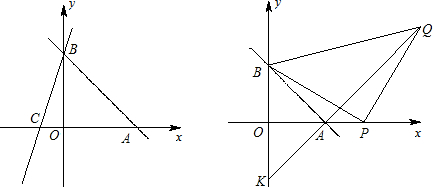
直线AB:![]() 分别与x、y轴交于A
分别与x、y轴交于A ![]() 、B两点,过点B的直线交x轴负半轴于C,且
、B两点,过点B的直线交x轴负半轴于C,且![]() ;
;
(1)求直线BC的解析式;
(2)直线EF:![]() (
(![]() )交AB于E,交BC于点F,交x轴于D,是否存在这样的直线EF,使得
)交AB于E,交BC于点F,交x轴于D,是否存在这样的直线EF,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由?
的值;若不存在,说明理由?
(3)P为A点右侧x轴上的一动点,以P为直角顶点、BP为腰在第一象限内作等腰直角三角形△BPQ,连结QA并延长交y轴于点K。当P点运动时,K点的位置是否发生变化?如果不变请求出它的坐标;如果变化,请说明理由。
(1)y = 3x + 6
(2)![]()
(3)K(0,-6)
解析:(1)解:由已知:0 = ![]() ,∴b = -6,∴AB:
,∴b = -6,∴AB:![]() 。
。
∴B(0,6)∴OB=6
∵OB︰OC = 3︰1,![]() ,
,
∴C(-2,0)。∴BC:y = 3x + 6。
(2)解:过E、F分别作EM ⊥x轴,FN ⊥x轴,则∠EMD=∠FND=90°。
∵S△EBD = S△FBD
∴DE = DF。又∠NDF = ∠EDM,
∴△NFD ≌△EDM,∴FN = ME。联立![]() 得
得![]() ,联立
,联立![]() 得
得![]() 。∵FN =-yF , ME =
。∵FN =-yF , ME =  ,∴
,∴![]() 。
。
∵k ≠ 0,∴![]() ,∴
,∴![]() 。
。
(3)不变化K(0,-6)。过Q作QH ⊥x轴于H,易证△BOP ≌△HPQ。∴PH = BO,OP = QH ,∴PH+ PO = BO + QH,即OA + AH = BO + QH。又OA = OB,∴AH = QH ,
∴△AHQ是等腰直角三角形,∴∠QAH = 45°,∴∠OAK = 45°,
∴△AOK为等腰直角三角形,∴OK = OA = 6,∴K(0,-6)


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
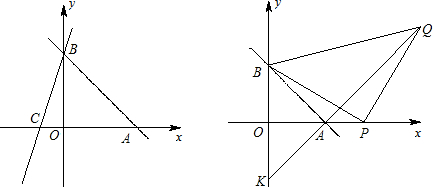
查看答案和解析>>
科目:初中数学 来源:2012年新疆阿拉尔市鹏源教育中考数学模拟试卷(二)(解析版) 题型:选择题
 x+1分别与x轴、y轴交于点A,点B,直线CD:y=x+b分别与x轴,y轴交于点C,点D.直线AB与CD相交于点P,已知S△ABD=4,则点P的坐标是( )
x+1分别与x轴、y轴交于点A,点B,直线CD:y=x+b分别与x轴,y轴交于点C,点D.直线AB与CD相交于点P,已知S△ABD=4,则点P的坐标是( )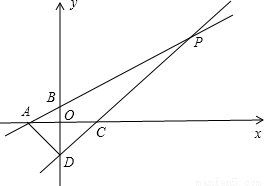
 )
) ,
, )
)查看答案和解析>>
科目:初中数学 来源:2009年湖北省鄂州市中考数学试卷(解析版) 题型:选择题
 x+1分别与x轴、y轴交于点A,点B,直线CD:y=x+b分别与x轴,y轴交于点C,点D.直线AB与CD相交于点P,已知S△ABD=4,则点P的坐标是( )
x+1分别与x轴、y轴交于点A,点B,直线CD:y=x+b分别与x轴,y轴交于点C,点D.直线AB与CD相交于点P,已知S△ABD=4,则点P的坐标是( )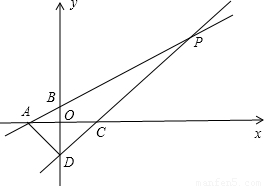
 )
) ,
, )
)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com