
 某校有一块四边形草地如图所示,已经测量出它的四条边长AB=6m,AD=8m,BC=26m,CD=24m,且∠A=90°
某校有一块四边形草地如图所示,已经测量出它的四条边长AB=6m,AD=8m,BC=26m,CD=24m,且∠A=90°分析 (1)连接BD,由勾股定理求出BD即可;
(2)由勾股定理的逆定理证出△BCD是直角三角形,∠BDC=90°,四边形ABCD的面积=△ABD的面积+△BCD的面积,即可得出结果.
解答 解:(1)连接BD,如图所示: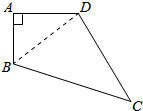
∵∠A=90°,
∴BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10(m);
(2)∵102+242=262,
∴BD2+CD2=BC2,
∴△BCD是直角三角形,∠BDC=90°,
∴四边形ABCD的面积=△ABD的面积+△BCD的面积=$\frac{1}{2}$AB•AD+$\frac{1}{2}$BD×CD
=$\frac{1}{2}$×6×8+$\frac{1}{2}$×10×24=144(cm2).
点评 本题考查了勾股定理、勾股定理的逆定理、直角三角形面积的计算方法;熟练掌握勾股定理和勾股定理的逆定理,证明三角形是直角三角形是解决问题的关键.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:解答题
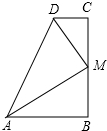 如图,∠B=∠C=90°,M是BC中点,DM平分∠ADC
如图,∠B=∠C=90°,M是BC中点,DM平分∠ADC查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{(-25)×(-36)}=\sqrt{-25}×\sqrt{-36}$=-5×(-6)=30 | B. | $\sqrt{8{a}^{4}b}=4{a}^{2}$b | ||
| C. | $\sqrt{{5}^{2}+{4}^{2}}$=5+4=9 | D. | $\sqrt{{15}^{2}-{12}^{2}}=\sqrt{15+12}×\sqrt{15-12}=9$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | A+B | B. | A-B | C. | 3A-B | D. | 3B-A |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com