
分析 联立方程得出关于x的二元一次方程,根据△=(k+1)2+$\frac{1}{3}$>0,判定一次函数y=kx-($\frac{k}{2}$-$\frac{1}{3}$)和二次函数y=x2必有两个不同的交点;然后分两种情况讨论,判定两种情况都不存在,从而证得结论.
解答 解:∵y=kx-($\frac{k}{2}$-$\frac{1}{3}$),
∴k≠0,
联立$\left\{\begin{array}{l}{y=kx-(\frac{k}{2}-\frac{1}{3})}\\{y={x}^{2}}\end{array}\right.$,
∴x2-kx+($\frac{k}{2}$-$\frac{1}{3}$)=0,
∵△=k2-4×1×($\frac{k}{2}$-$\frac{1}{3}$)=(k+1)2+$\frac{1}{3}$>0,
∴一次函数y=kx-($\frac{k}{2}$-$\frac{1}{3}$)和二次函数y=x2必有两个不同的交点,
①当k>0时,一次函数y=kx-($\frac{k}{2}$-$\frac{1}{3}$)和二次函数y=x2的交点在单位正方形OABC外部,
则x=0时,y>0,当x=1时,y>1,
即$\left\{\begin{array}{l}{-\frac{k}{2}+\frac{1}{3}>0}\\{\frac{k}{2}+\frac{1}{3}>1}\end{array}\right.$
解得不等式组无解,
所以,此种情况不存在;
②当k<0时,一次函数y=kx-($\frac{k}{2}$-$\frac{1}{3}$)和二次函数y=x2的交点在单位正方形OABC外部,
则x=0时,y<0,当x=1时,y>1,
即$\left\{\begin{array}{l}{-\frac{k}{2}+\frac{1}{3}<0}\\{\frac{k}{2}+\frac{1}{3}>0}\end{array}\right.$
解得k$>\frac{4}{3}$,这与k<0矛盾,
所以,此种情况也不存在;
综上,无论k为何值,一次函数y=kx-($\frac{k}{2}$-$\frac{1}{3}$)和二次函数y=x2必会有一个交点在单位正方形OABC内部.
点评 本题考查了二次函数的性质,直线和抛物线的交点问题,分类讨论思想的运用是解题的关键.


科目:初中数学 来源: 题型:选择题
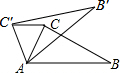 如图,在△ABC中,∠CAB=70°,将△ABC绕点A按逆时针方向旋转一个锐角α到△AB′C′的位置,连接CC′,若CC′∥AB,则旋转角α的度数为( )
如图,在△ABC中,∠CAB=70°,将△ABC绕点A按逆时针方向旋转一个锐角α到△AB′C′的位置,连接CC′,若CC′∥AB,则旋转角α的度数为( )| A. | 40° | B. | 50° | C. | 30° | D. | 35° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,△ABC是等腰三角形,BC=BA,B点坐标为(1,$\sqrt{3}$),C点坐标为(0,0),且S△ABC=$\sqrt{3}$.将△ABC沿x轴向右平移$\sqrt{2}$个单位长,使点A、B、C分别平移到A′,B′,C′.
如图,在平面直角坐标系中,△ABC是等腰三角形,BC=BA,B点坐标为(1,$\sqrt{3}$),C点坐标为(0,0),且S△ABC=$\sqrt{3}$.将△ABC沿x轴向右平移$\sqrt{2}$个单位长,使点A、B、C分别平移到A′,B′,C′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
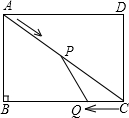 在矩形ABCD中,AB=3米,BC=4米,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1米/秒的速度从点C出发,沿CB向点B移动,设P、Q两点同时移动的时间为t秒(0<t<2.5).
在矩形ABCD中,AB=3米,BC=4米,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1米/秒的速度从点C出发,沿CB向点B移动,设P、Q两点同时移动的时间为t秒(0<t<2.5).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
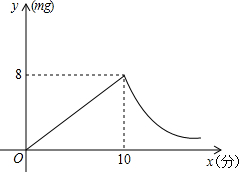 为预防“手足口病”,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(分钟)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题:
为预防“手足口病”,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(分钟)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
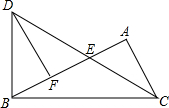 如图,在△ABC中,∠BAC=90°,过点B作BC的垂线交∠ACB的角平分线于点D,CD与AB边交于点E,过D作DF⊥AB于点F.
如图,在△ABC中,∠BAC=90°,过点B作BC的垂线交∠ACB的角平分线于点D,CD与AB边交于点E,过D作DF⊥AB于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点C在线段AB上,AC=6cm,MB=10cm,点M、N分别为AC、BC的中点.
如图,点C在线段AB上,AC=6cm,MB=10cm,点M、N分别为AC、BC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com