
����Ŀ��ij�̳�Ҫ��Ӫһ�������е��ľߣ�����Ϊ![]() Ԫ
Ԫ![]() ������Ӫ���η��֣������۵�����
������Ӫ���η��֣������۵�����![]() Ԫʱ��ÿ���������Ϊ
Ԫʱ��ÿ���������Ϊ![]() �������۵���ÿ����
�������۵���ÿ����![]() Ԫ��ÿ����������ͼ���
Ԫ��ÿ����������ͼ���![]() ����
����
��1��д���̳����������ľߣ�ÿ�����õ���������![]() (Ԫ)�����۵���
(Ԫ)�����۵���![]() (Ԫ)֮��ĺ�����ϵʽ��
(Ԫ)֮��ĺ�����ϵʽ��
��2�������۵��۶�Ϊ����Ԫʱ�����ľ�ÿ���������������������Ϊ����Ԫ��
��3���̳���Ӫ���������������������![]() ��
��![]() ����Ӫ��������
����Ӫ��������
����![]() �����ľߵ����۵��۸��ڽ��ۣ���������
�����ľߵ����۵��۸��ڽ��ۣ���������![]() Ԫ��
Ԫ��
����![]() ��ÿ��������������
��ÿ��������������![]() ������ÿ���ľߵ���������Ϊ
������ÿ���ľߵ���������Ϊ![]() Ԫ��
Ԫ��
��Ƚ����ַ��������������ߣ���˵�����ɣ�
���𰸡���1��![]() ����2�������۵��۶�Ϊ
����2�������۵��۶�Ϊ![]() Ԫʱ�����ľ�ÿ���������������������Ϊ
Ԫʱ�����ľ�ÿ���������������������Ϊ![]() Ԫ����3��
Ԫ����3��![]() ���������������ߣ����ɼ�������
���������������ߣ����ɼ�������
��������
��1����������=�����۵���-���ۣ������������г�������ϵʽ���ɣ�
��2�����ݣ�1��ʽ�г��ĺ�����ϵʽ�������䷽�������ֵ��
��3���ֱ��������A��B��x��ȡֵ��Χ��Ȼ��ֱ����A��B�������������Ȼ����бȽϣ�
�⣺��1��������ã�������![]() ��
��
��![]()
![]() ��
��
��2��![]() ��
��
![]() ��
��
![]() ����ͼ�����£�
����ͼ�����£�![]() �����ֵ��
�����ֵ��
��![]() ʱ��
ʱ��![]() ��
��
�𣺵����۵��۶�Ϊ![]() Ԫʱ�����ľ�ÿ���������������������Ϊ
Ԫʱ�����ľ�ÿ���������������������Ϊ![]() Ԫ��
Ԫ��
��3��![]() ���������������ߣ��������£�
���������������ߣ��������£�
��![]() ������
������![]() ��
��
![]() ����
����![]() ����ͼ��ĶԳ���Ϊֱ��
����ͼ��ĶԳ���Ϊֱ��![]() ���ҿ������£�
���ҿ������£�
![]() ��
��![]() ʱ��
ʱ��![]() �����ֵ��
�����ֵ��
��ʱ![]() ��
��
��![]() ������
������![]()
��ã�![]() ��
��
![]() ����
����![]() ����ͼ��ĶԳ���Ϊֱ��
����ͼ��ĶԳ���Ϊֱ��![]() ���ҿ������£�
���ҿ������£�
![]() ��
��![]() ʱ��
ʱ��![]() �����ֵ��
�����ֵ��
��ʱ![]() ��
��
![]() ��
��
![]() ���������������ߣ�
���������������ߣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
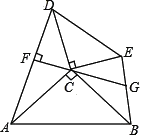
����Ŀ����ͼ���� C Ϊ Rt��ACB �� Rt��DCE �Ĺ���������ACB=��DCE=90������ �� AD��BE������ C �� CF��AD �ڵ� F���ӳ� FC �� BE �ڵ� G���� AC=BC=25��CE=15�� DC=20����![]() ��ֵΪ___________��
��ֵΪ___________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
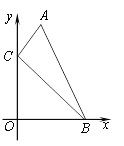
����Ŀ����ͼ����ֱ������ϵ�У���A��B������ֱ�Ϊ��1��4���ͣ�3��0������C��y���ϵ�һ�����㣬��A��B��C���㲻��ͬһ��ֱ���ϣ�����ABC���ܳ���Сʱ����C��������____________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
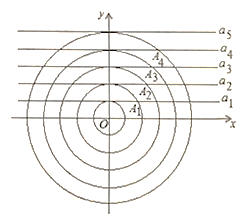
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ�У�һ��ͬ��Բ��Բ��Ϊ����ԭ��![]() ,���ǵİ뾶�ֱ�Ϊ
,���ǵİ뾶�ֱ�Ϊ![]() ����������
����������![]() "���ε���; һ��ƽ����
"���ε���; һ��ƽ����![]() , �����ֱ��
, �����ֱ��![]() ��������õ��Բ���У����뾶Ϊ
��������õ��Բ���У����뾶Ϊ![]() ��Բ��
��Բ��![]() �ڵ�һ�����ڽ��ڵ�
�ڵ�һ�����ڽ��ڵ�![]() ,�뾶Ϊ
,�뾶Ϊ![]() ��Բ��
��Բ��![]() �ڵ��������ཻ�ڵ�
�ڵ��������ཻ�ڵ�![]() ���뾶Ϊ
���뾶Ϊ![]() ��Բ��
��Բ��![]() �ڵ�һ�������ཻ�ڵ�
�ڵ�һ�������ཻ�ڵ�![]() ���մ˹��ɣ����
���մ˹��ɣ����![]() ��������( )
��������( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
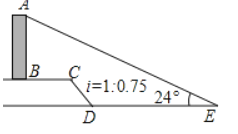
����Ŀ����ͼ��![]() ��һ��ֱ��ˮƽ��Ľ����ijͬѧ�ӽ������
��һ��ֱ��ˮƽ��Ľ����ijͬѧ�ӽ������![]() ����������ˮƽ������������
����������ˮƽ������������![]() �����
�����![]() �پ������¶�(���±�)Ϊ
�پ������¶�(���±�)Ϊ![]() �³�Ϊ
�³�Ϊ![]() ��б��
���![]() �����
�����![]() Ȼ������ˮƽ������������
Ȼ������ˮƽ������������![]() �����
�����![]() ����ͬһƽ����)����
����ͬһƽ����)����![]() ����ý����ﶥ��
����ý����ﶥ��![]() ������Ϊ
������Ϊ![]() ������
������![]() �ĸ߶ȣ� (�ο����ݣ�
�ĸ߶ȣ� (�ο����ݣ�![]() ��
��![]()
![]() )
)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�![]() ��AC=4��BC=3����D��б��AB���е㣮 �Ե�DΪ������
��AC=4��BC=3����D��б��AB���е㣮 �Ե�DΪ������![]() ������DM��DN�ֱ�AC��CB�ڵ�E��F��
������DM��DN�ֱ�AC��CB�ڵ�E��F��
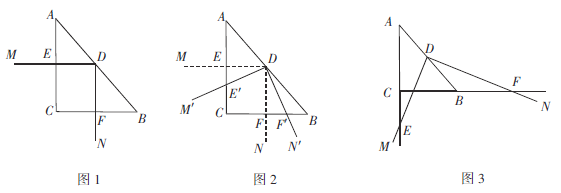
����
��1����ͼ1����![]() �������Ӹ����ߣ�ͼ1���������ABC���Ƶ�������Ϊ ��
�������Ӹ����ߣ�ͼ1���������ABC���Ƶ�������Ϊ ��![]() ��
��
����̽����
��2������1���е�![]() ��ͼ1 ��λ�ÿ�ʼ�Ƶ�D����ʱ�뷽����ת���õ�
��ͼ1 ��λ�ÿ�ʼ�Ƶ�D����ʱ�뷽����ת���õ�![]() ����ͼ2��������
����ͼ2��������![]() �ֱ�
�ֱ�![]() �ڵ�
�ڵ�![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��
��չ���죺
��3����ͼ3��![]() �У�
�У�![]() ��AC=m��BC=n����D��б��AB���е㣬�Ե�DΪ������
��AC=m��BC=n����D��б��AB���е㣬�Ե�DΪ������![]() ������
������![]() �ֱ�
�ֱ�![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ����
����![]() ��ֵΪ_______________�����ú�
��ֵΪ_______________�����ú�![]() �Ĵ���ʽ��ʾ��ֱ�ӻشɣ�
�Ĵ���ʽ��ʾ��ֱ�ӻشɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB��ԲO��ֱ������CD��AB������ΪH����ACƽ�е�ԲO��һ�����߽�CD���ӳ����ڵ�M����AB���ӳ����ڵ�E���е�ΪF������AF��CD�ڵ�N��
��1����֤��CA=CN��
��2������DF����cos��DFA=![]() ��AN=
��AN=![]() ����ԲO��ֱ���ij��ȣ�
����ԲO��ֱ���ij��ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ƽ��ֱ������ϵ�У������ߵĶ�������Ϊ![]() ����C��0��6������������y�Ľ��㣮
����C��0��6������������y�Ľ��㣮
��1������������x��Ľ���A��B�����꣨A��B����ߣ���
��2����ֱ��y��h��hΪ������0��h��6����ֱ��BC���ڵ�D����y���ڵ�E����AC���ڵ�F����AE������M������Ϊ����2��0����
����hΪ��ֵʱ����AEF�����S���
���ʣ��Ƿ����������ֱ��y��h��ʹ��BDM�ǵ��������Σ������ڣ������h��ֵ�͵�D�����ꣻ�������ڣ���˵�����ɣ�
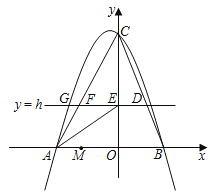
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com