
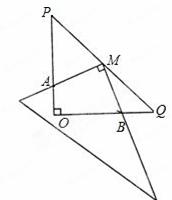
如图,在Rt△POQ中,OP=OQ=5,M是PQ的中点,把一三角尺的直角顶点放在点M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.
(1)求证:MA=MB;
(2)探究:在旋转三角尺的过程中,四边形AOBM的面积是否发生变化?若发生变化,请说明理由;若不发生变化,请求出四边形AOBM的面积.
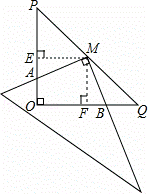
1)证明:如图,过点M作ME⊥OP于点E,作MF⊥OQ于点F,
∵∠O=90°,
∴四边形OEMF是矩形,
∵M是PQ的中点,OP=OQ=4,∠O=90°,
∴ME=![]() OQ=2,MF=
OQ=2,MF=![]() OP=2,
OP=2,
∴ME=MF,
∴四边形OEMF是正方形,
∵∠AME+∠AMF=90°,∠BMF+∠AMF=90°,
∴∠AME=∠BMF,
在△AME和△BMF中,
 ,
,
∴△AME≌△BMF(ASA),
∴MA=MB;
(2)解:四边形AOBM的面积不发生变化;
理由:由(1)得出:AE=FB,OF=FQ=OE,
∴BQ=FQ﹣BF=EO﹣AE=AO,
∴PA+BQ=PO=5,
∵四边形AOBM的面积为:S△POQ﹣S△MPA﹣S△MQB=![]() ×PO×QO﹣
×PO×QO﹣![]() (PA+BQ)×ME=
(PA+BQ)×ME=![]() ×5×5﹣
×5×5﹣![]() ×5×
×5×![]() =
=![]() .
.


科目:初中数学 来源: 题型:
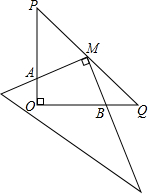 如图,在Rt△POQ中,OP=OQ=5,M是PQ的中点,把一三角尺的直角顶点放在点M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.
如图,在Rt△POQ中,OP=OQ=5,M是PQ的中点,把一三角尺的直角顶点放在点M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.查看答案和解析>>
科目:初中数学 来源:2013届江苏省江阴初级中学九年级上学期期末考试数学试卷(带解析) 题型:填空题
探究:如图,在Rt△POQ中OP=OQ=4,将一把三角尺的直角顶点放在PQ中点M处,以M为旋转中心旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B,连接AB,则△AOB周长的最小值是 .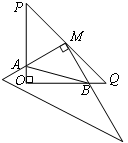
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省九年级上学期期末考试数学试卷(解析版) 题型:填空题
探究:如图,在Rt△POQ中OP=OQ=4,将一把三角尺的直角顶点放在PQ中点M处,以M为旋转中心旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B,连接AB,则△AOB周长的最小值是 .

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
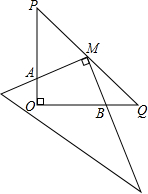 如图,在Rt△POQ中,OP=OQ,M是PQ的中点,把一三角尺的直角顶点放在M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.求证:MA=MB.
如图,在Rt△POQ中,OP=OQ,M是PQ的中点,把一三角尺的直角顶点放在M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.求证:MA=MB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com