
【题目】已知△OBF 是直角三角形,∠BFO=90°,∠BOF=30°,△AOB 是等边三角形,OB=4,点 A 与点 F 位于直线 OB 的异侧.
(Ⅰ)如图①,求 BF 及 OF 的长;
(Ⅱ)点 P 是直线OF 上的一个动点,连接 AP,以点 A 为旋转中心,把△AOP 逆时针旋转,使边 AO 与 AB 重合,得△ABD.
①如图②,求在点 P 运动过程中,使点 D 落在线段 OF 上时 OP 的长;
②求在点 P 运动过程中,使点 P 落在线段 OF 上,且△OPD 的面积等于![]() 时 OP 的长(直接写出结果即可).
时 OP 的长(直接写出结果即可).

【答案】(1)![]() (2)①
(2)① ![]() ②
②![]()
【解析】
(I)如图①中,解直角三角形△OBF 即可;
(Ⅱ)①只要证明△PAD 是等边三角形,OA⊥PD 即可解决问题;
②如图③中,过点 B 作 BE⊥OA 于点 E,过点 D 作 DH⊥x 轴于点 H,延长 EB 交 DH 于点 G,则 BG⊥DH.根据三角形的面积公式构建方程即可解决问题;
(I)如图①中,
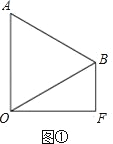
在 Rt△BOF 中,∵∠F=90°,∠BOF=30°,OB=4,
∴BF=![]() OB=2,OF=
OB=2,OF=![]() =2
=2![]() .
.
(Ⅱ)①如图②中,
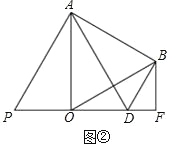
∵△AOB 是等边三角形,
∴OA=OB=AB=4,∠OAB=∠AOB=60°
由旋转可知:∠PAD=∠OAB=60°,AP=AD,
∴△APD 是等边三角形,
∵∠AOD=∠AOB+∠BOF=90°,
∴OA⊥PD,
∴OP=OD,∠PAO=∠DAO=30°,
∴OP=OAtan30°= ![]()
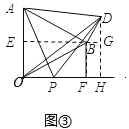 ②如图③中,过点 B 作 BE⊥OA 于点 E,过点 D 作 DH⊥x 轴于点 H,延长 EB 交 DH 于点 G,则 BG⊥DH.
②如图③中,过点 B 作 BE⊥OA 于点 E,过点 D 作 DH⊥x 轴于点 H,延长 EB 交 DH 于点 G,则 BG⊥DH.
设 BD=OP=x,
在 Rt△DBG 中,∠DBG=60°,
∴DG=BDsin60°= ![]() x.
x.
∴DH=2+ ![]() x.
x.
∵△OPD 的面积等于 ![]() ,
,
∴ ![]() x(2+
x(2+ ![]() x)=
x)=![]() ,
,
整理得:![]() x2+4x﹣
x2+4x﹣![]() =0,
=0,
解得:x= ![]() 或
或 ![]() (舍去).
(舍去).
∴OP= ![]() .
.


科目:初中数学 来源: 题型:
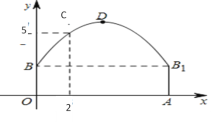
【题目】如图隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m.按照图中所示的直角坐标系,抛物线可以用y=![]() x2+bx+c表示,且抛物线上的点C到OB的水平距离为2m,到地面OA的距离为5m.
x2+bx+c表示,且抛物线上的点C到OB的水平距离为2m,到地面OA的距离为5m.
(1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)该隧道内设双行道,一辆货车高4m,宽2.5m,能否安全通过,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在改革开放30年纪念活动中,某校学生会就同学们对我国改革开放30年所取得的辉煌成就的了解程度进行了随机抽样调查,并将调查结果绘制成如图所示的统计图的一部分.
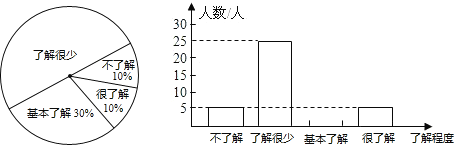
根据统计图中的信息,解答下列问题:
(1)本次抽样调查的样本容量是 .调查中“了解很少”的学生占 %;
(2)补全条形统计图;
(3)若全校共有学生1300人,那么该校约有多少名学生“很了解”我国改革开放30年来取得的辉煌成就.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰直角三角形ABC和等腰直角三角形ADE中,∠BAC=∠DAE=90°,AB=4,AE=2,其中△ABC固定,△ADE绕点A作360°旋转,点F、M、N分别为线段BE、BC、CD的中点,连接MN、NF.
问题提出:(1)如图1,当AD在线段AC上时,则∠MNF的度数为 ,线段MN和线段NF的数量关系为 ;
深入讨论:(2)如图2,当AD不在线段AC上时,请求出∠MNF的度数及线段MN和线段NF的数量关系;
拓展延伸:(3)如图3,△ADE持续旋转过程中,若CE与BD交点为P,则△BCP面积的最小值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学考试中,小明有一道选择题(只能在四个选项A、B、C、D中选一个)不会做,便随机选了一个答案;小亮有两道选择题都不会做,他也随机选了两个答案.
(1)小明随机选的这个答案,答对的概率是 ;
(2)通过画树状图或列表法求小亮两题都答对概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从﹣1,﹣2,﹣3,﹣4,﹣5,﹣6中任取一个数作为k的值,则能使分式方程![]() 有非负实数解且使二次函数y=x2+2x﹣k﹣1的图象与x轴无交点的概率为( )
有非负实数解且使二次函数y=x2+2x﹣k﹣1的图象与x轴无交点的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.0
D.0
查看答案和解析>>
科目:初中数学 来源: 题型:
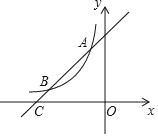
【题目】如图,一次函数y=x+4的图象与反比例函数y=![]() (k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求a,k的值及点B的坐标;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,直接写出点P的坐标.
S△BOC,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
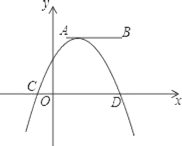
【题目】如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x+m)2+n的顶点在线段AB上,与x轴交于C,D两点(C在D的左侧),点C的横坐标最小值为﹣3,则点D的横坐标的最大值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com