
【题目】如图是甲、乙两名射击运动员的10次射击测试成绩的折线统计图.
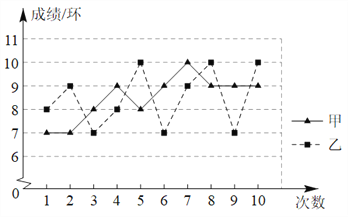
(1)根据折线图把下列表格补充完整;
运动员 | 平均数 | 中位数 | 众数 |
甲 | 8.5 | 9 | |
乙 | 8.5 |
(2)根据上述图表运用所学统计知识对甲、乙两名运动员的射击水平进行评价并说明理由.
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 为坐标原点,正方形
为坐标原点,正方形![]() 与长方形
与长方形![]() 的位置如图所示,点
的位置如图所示,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() ,
,![]() 在
在![]() 轴的负半轴上(点
轴的负半轴上(点![]() 在点
在点![]() 的右侧),点
的右侧),点![]() 的坐标为
的坐标为![]() ,
,![]() ,实数
,实数![]() ,
,![]() 的值满足
的值满足![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)长方形![]() 以每秒1个单位长度的速度向右平移
以每秒1个单位长度的速度向右平移![]() (
(![]() )秒得到矩形
)秒得到矩形![]() ,点
,点![]() ,
,![]() ,
,![]() ,
,![]() 分别为点
分别为点![]() ,
,![]() ,
,![]() ,
,![]() 平移后的对应点,设矩形
平移后的对应点,设矩形![]() 与正方形
与正方形![]() 重合部分的面积为
重合部分的面积为![]() ,用含
,用含![]() 的式子表示
的式子表示![]() ,并直接写出相应的
,并直接写出相应的![]() 的范围;
的范围;
(3)在(2)的条件下,在长方形![]() 出发运动的同时,点
出发运动的同时,点![]() 从点
从点![]() 出发,沿正方形的边以每秒2个单位长度的速度顺时针方向运动(即
出发,沿正方形的边以每秒2个单位长度的速度顺时针方向运动(即![]() ),连接
),连接![]() ,
,![]() ,当三角形
,当三角形![]() 的面积为15时,求
的面积为15时,求![]() 时相应的
时相应的![]() 值,并直接写出此时刻
值,并直接写出此时刻![]() 值及点
值及点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初二年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初二学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:
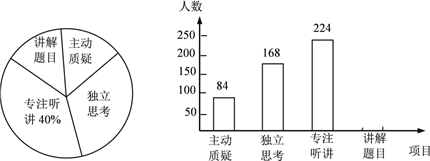
(1)在这次评价中,一共抽查了 名学生;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为 度;
(3)请将频数分布直方图补充完整;
(4)如果全市有6000名初二学生,那么在试卷评讲课中,“独立思考”的初二学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“作以已知线段为斜边的等腰直角三角形”的尺规作图过程.
已知:线段![]() .
.
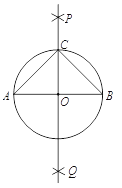
![]()
求作:以![]() 为斜边的一个等腰直角三角形
为斜边的一个等腰直角三角形![]() .
.
作法:如图,
(1)分别以点![]() 和点
和点![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧,两弧相交于
的长为半径作弧,两弧相交于![]() ,
,![]() 两点;
两点;
(2)作直线![]() ,交
,交![]() 于点
于点![]() ;
;
(3)以![]() 为圆心,
为圆心,![]() 的长为半径作圆,交直线
的长为半径作圆,交直线![]() 于点
于点![]() ;
;
(4)连接![]() ,
,![]() .
.
则![]() 即为所求作的三角形.
即为所求作的三角形.
请回答:在上面的作图过程中,①![]() 是直角三角形的依据是________;②
是直角三角形的依据是________;②![]() 是等腰三角形的依据是__________.
是等腰三角形的依据是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(方法回顾)证明:三角形中位线定理.
已知:如图1,![]() 中,D、E分别是AB、AC的中点.
中,D、E分别是AB、AC的中点.
求证:![]() ,
,![]() .
.
证明:如图1,延长DE到点F,使得![]() ,连接CF;
,连接CF;
请继续完成证明过程;

(2)(问题解决)
如图2,在矩形ABCD中,E为AD的中点,G、F分别为AB、CD边上的点,若![]() ,
,![]() ,
,![]() ,求GF的长.
,求GF的长.
(3)(思维拓展)
如图3,在梯形ABCD中,![]() ,
,![]() ,
,![]() ,E为AD的中点,G、F分别为AB、CD边上的点,若
,E为AD的中点,G、F分别为AB、CD边上的点,若![]() ,
,![]() ,
,![]() ,求GF的长.
,求GF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的轨道上有两个点甲与乙,开始时甲在A处,乙在C处,它们沿着正方形轨道顺时针同时出发,甲的速度为每秒1 cm,乙的速度为每秒5 cm,已知正方形轨道ABCD的边长为2 cm,则乙在第2 020次追上甲时的位置在( )
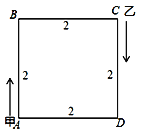
A.AB上B.BC上
C.CD上D.AD上
查看答案和解析>>
科目:初中数学 来源: 题型:
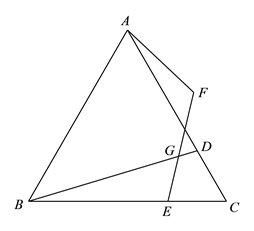
【题目】如图,在等边![]() 中,
中, ![]() 分别是边
分别是边![]() 上的点,且
上的点,且![]() ,
,![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 对称,连接
对称,连接![]() ,
,![]() 交
交![]() 于
于![]() .
.
(1)连接![]() ,则
,则![]() 之间的数量关系是 ;
之间的数量关系是 ;
(2)若![]() ,求
,求![]() 的大小(用
的大小(用![]() 的式子表示)
的式子表示)
(2)用等式表示线段![]() 和
和![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图象(折线OEFPMN)描述了某汽车在行驶过程中速度与时间的函数关系,下列说法中错误的是( )

A. 第3分时汽车的速度是40千米/时
B. 第12分时汽车的速度是0千米/时
C. 从第3分到第6分,汽车行驶了120千米
D. 从第9分到第12分,汽车的速度从60千米/时减少到0千米/时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向点B以1cm/s的速度移动;同时,点Q从点B沿边BC向点C以2cm/s的速度移动.

(1)问几秒后△PBQ的面积等于8cm2?
(2)是否存在这样的时刻,使![]() =8cm2,试说明理由.
=8cm2,试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com