
| A. | E、F、G | B. | F、G、H | C. | G、H、E | D. | H、E、F |
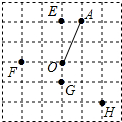
分析 根据网格中两点间的距离分别求出,OE,OF,OG,OH然后和OA比较大小.最后得到哪些树需要移除.
解答 解:∵OA=$\sqrt{1+{2}^{2}}$=$\sqrt{5}$,
∴OE=2<OA,所以点E在⊙O内,
OF=2<OA,所以点F在⊙O内,
OG=1<OA,所以点G在⊙O内,
OH=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$>OA,所以点H在⊙O外,
故选A
点评 此题是点与圆的位置关系,主要考查了网格中计算两点间的距离,比较线段长短的方法,计算距离是解本题的关键.点到圆心的距离小于半径,点在圆内,点到圆心的距离大于半径,点在圆外,点到圆心的距离大于半径,点在圆内.


科目:初中数学 来源: 题型:解答题
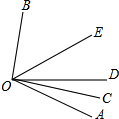 如图,OC是∠AOD的平分线,OE是∠BOD的平分线.
如图,OC是∠AOD的平分线,OE是∠BOD的平分线.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
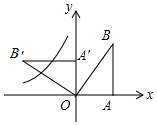 如图,在平面直角坐标系中,Rt△OAB的顶点A、B的坐标分别是(2,0),(2,4),将△OAB绕点O逆时针方向旋转90°,得到△OA′B′,函数y=$\frac{k}{x}$(x<0)的图象过A′B′的中点C,则k的值为( )
如图,在平面直角坐标系中,Rt△OAB的顶点A、B的坐标分别是(2,0),(2,4),将△OAB绕点O逆时针方向旋转90°,得到△OA′B′,函数y=$\frac{k}{x}$(x<0)的图象过A′B′的中点C,则k的值为( )| A. | 4 | B. | -4 | C. | 8 | D. | -8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | b≥$\frac{5}{4}$ | B. | b≥1或b≤-1 | C. | b≥2 | D. | 1≤b≤2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.
如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )
某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )| A. | 该村人均耕地面积随总人口的增多而增多 | |
| B. | 该村人均耕地面积y与总人口x成正比例 | |
| C. | 若该村人均耕地面积为2公顷,则总人口有100人 | |
| D. | 当该村总人口为50人时,人均耕地面积为1公顷 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
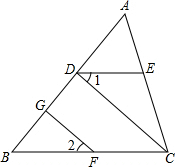 已知:如图,CD⊥AB,FG⊥AB,垂足分别为D、G,点E在AC上,且∠1=∠2,求证:∠B=∠ADE
已知:如图,CD⊥AB,FG⊥AB,垂足分别为D、G,点E在AC上,且∠1=∠2,求证:∠B=∠ADE查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com