
【题目】思维探索:
在正方形ABCD中,AB=4,∠EAF的两边分别交射线CB,DC于点E,F,∠EAF=45°.
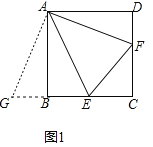
(1)如图1,当点E,F分别在线段BC,CD上时,△CEF的周长是 ;
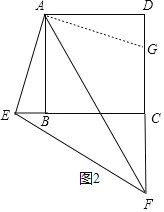
(2)如图2,当点E,F分别在CB,DC的延长线上,CF=2时,求△CEF的周长;
拓展提升:
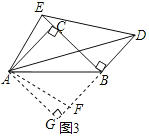
如图3,在Rt△ABC中,∠ACB=90°,CA=CB,过点B作BD⊥BC,连接AD,在BC的延长线上取一点E,使∠EDA=30°,连接AE,当BD=2,∠EAD=45°时,请直接写出线段CE的长度.

【答案】思维探索:(1)8;(2)12;拓展提升:CE=![]() ﹣1.
﹣1.
【解析】
思维探索:(1)利用旋转的性质,证明△AGE≌△AFE即可;
(2)把△ABE绕点A逆时针旋转90°到AD,交CD于点G,证明△AEF≌△AGF即可求得EF=DF﹣BE;
拓展提升:如图3,过A作AG⊥BD交BD的延长线于G,推出四边形ACBG是矩形,得到矩形ACBG是正方形,根据正方形的性质得到AC=AG,∠CAG=90°,在BG上截取GF=CE,根据全等三角形的性质得到AE=AF,∠EAC=∠FAG,∠ADF=∠ADE=30°,解直角三角形得到DE=DF=4,BE=2![]() ,设CE=x,则GF=CE=x,BC=BG=2
,设CE=x,则GF=CE=x,BC=BG=2![]() ﹣x,根据线段的和差即可得到结论.
﹣x,根据线段的和差即可得到结论.
思维探索:
(1)如图1,将△ADF绕点A顺时针旋转90°得到△ABG,
∴GB=DF,AF=AG,∠BAG=∠DAF,
∵四边形ABCD为正方形,
∴∠BAD=90°,
∵∠EAF=45°,
∴∠BAE+∠DAF=45°,
∴∠BAG+∠BAE=45°=∠EAF,
在△AGE和△AFE中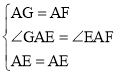
∴△AGE≌△AFE(SAS),
∴GE=EF,
∵GE=GB+BE=BE+DF,
∴EF=BE+DF,
∴△CEF的周长=CE+CF+EF=CE+BE+DF+CF=BC+CD=8,
故答案为:8;
(2)如,2,把△ABE绕点A逆时针旋转90°到AD,交CD于点G,
同(1)可证得△AEF≌△AGF,
∴EF=GF,且DG=BE,
∴EF=DF﹣DG=DF﹣BE,
∴△CEF的周长=CE+CF+EF=CE+CF+DF﹣BE=BC+DF+CF=4+4+2+2=12;
拓展提升:如图3,过A作AG⊥BD交BD的延长线于G,
∵BD⊥BC,∠ACB=90°,
∴∠ACB=∠CBG=∠G=90°,
∴四边形ACBG是矩形,
∵AC=BC,
∴矩形ACBG是正方形,
∴AC=AG,∠CAG=90°,
在BG上截取GF=CE,
∴△AEC≌△AGF(SAS),
∴AE=AF,∠EAC=∠FAG,
∵∠EAD=∠BAC=∠GAB=45°,
∴∠DAF=∠DAE=45°,
∵AD=AD,
∴△ADE≌△ADF(SAS),
∴∠ADF=∠ADE=30°,
∴∠BDE=60°,
∵∠DBE=90°,BD=2,
∴DE=DF=4,BE=2![]() ,
,
设CE=x,则GF=CE=x,BC=BG=2![]() ﹣x,
﹣x,
∴DG=2+2![]() ﹣x,
﹣x,
∴DG﹣FG=DF,
即2+2![]() ﹣x﹣x=4,
﹣x﹣x=4,
∴x=![]() ﹣1,
﹣1,
∴CE=![]() ﹣1.
﹣1.


科目:初中数学 来源: 题型:
【题目】阅读以下材料:对数的创始人是苏格兰数学家纳皮尔(J.Napier,1550年-1617年),纳皮尔发明对数是在指数概念建立之前,直到18世纪瑞士数学家欧拉(Euler,1707年-1783年)才发现指数与对数之间的联系.对数的定义:一般地,若![]() ,则
,则![]() 叫做以
叫做以![]() 为底
为底![]() 的对数,记作
的对数,记作![]() .比如指数式
.比如指数式![]() 可以转化为
可以转化为![]() ,对数式
,对数式![]() 可以转化为
可以转化为![]() .我们根据对数的定义可得到对数的一个性质:
.我们根据对数的定义可得到对数的一个性质:![]()
![]() .理由如下:设
.理由如下:设![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() ,由对数的定义得
,由对数的定义得![]() ,又因为
,又因为![]() ,所以
,所以![]() .解决以下问题:
.解决以下问题:
(1)将指数![]() 转化为对数式: .
转化为对数式: .
(2)仿照上面的材料,试证明:![]()
(3)拓展运用:计算![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
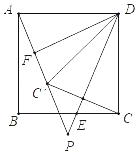
【题目】如图,在正方形ABCD中,E是边BC上的一动点(不与点B、C重合),连接DE、点C关于直线DE的对称点为C′,连接AC′并延长交直线DE于点P,F是AC′的中点,连接DF.
(1)求∠FDP的度数;
(2)连接BP,请用等式表示AP、BP、DP三条线段之间的数量关系,并证明;
(3)连接AC,若正方形的边长为![]() ,请直接写出△ACC′的面积最大值.
,请直接写出△ACC′的面积最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”;
理解:
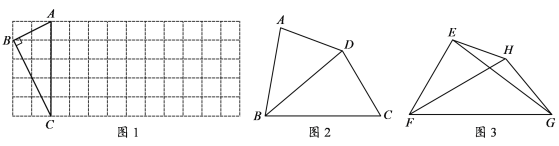
⑴ 如图1,△ABC的三个顶点均在正方形网格中的格点上,若四边形ABCD是以AC为“相似对角线”的四边形,请用无刻度的直尺在网格中画出点D(保留画图痕迹,找出3个即可);
⑵ 如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC. 请问BD是四边形ABCD的“相似对角线”吗?请说明理由;
运用:
⑶ 如图3,已知FH是四边形EFGH的“相似对角线”, ∠EFH=∠HFG=30°.连接EG,若△EFG的面积为![]() ,求FH 的长.
,求FH 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
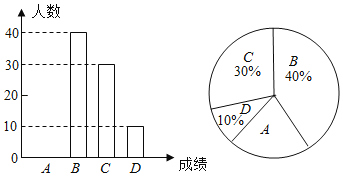
【题目】我校为了了解九年级学生身体素质测试情况,随机抽取了本校九年级部分学生的身体素质测试成绩为样本,按A(优秀)、B(良好)、C(合格)、D(不合格)四个等级进行统计,并将统计结果绘制成如图不完整的统计图,请你结合图表所给信息解答下列问题:
(1)请在答题卡上直接将条形统计图补充完整;
(2)扇形统计图中“B”部分所对应的圆心角的度数是 °;
(3)若我校九年级共有1500名学生参加了身体素质测试,试估计测试成绩合格以上(含合格)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀,让学生进行摸球试验,每次摸出一个球(放回),下表是活动进行中的一组统计数据.
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数m | 23 | 31 | 60 | 130 | 203 | 251 |
摸到黑球的频率 | 0.23 | 0.21 | 0.30 | 0.26 | 0.253 |
|
(1)![]() = ,根据上表数据估计从袋中摸出一个黑球的概率是 .
= ,根据上表数据估计从袋中摸出一个黑球的概率是 .
(2)估算袋中白球的个数为 .
(3)在(2)的条件下,若小强同学从袋中摸出两个球,用画树状图或列表的方法计算摸出的两个球都是白球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
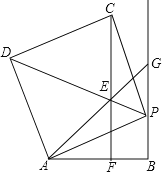
【题目】如图,线段AB=8,射线BG⊥AB,P为射线BG上一点,以AP为边作正方形APCD,且点C、D与点B在AP两侧,在线段DP上取一点E,使∠EAP=∠BAP,直线CE与线段AB相交于点F(点F与点A、B不重合).
(1)求证:△AEP≌△CEP;
(2)判断CF与AB的位置关系,并说明理由;
(3)求△AEF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,AB=4,点C是AB延长线上一点,且BC=2,点D是半圆的中点,点P是⊙O上任意一点.
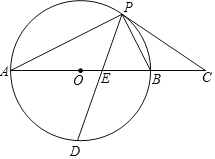
(1)当PD与AB交于点E且PC=CE时,求证:PC与⊙O相切;
(2)在(1)的条件下,求PC的长;
(3)点P是⊙O上动点,当PD+PC的值最小时,求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
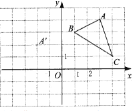
【题目】在平面直角坐标系中,![]() 的三个 顶点的位置如图所示, 点
的三个 顶点的位置如图所示, 点![]() ,现 将
,现 将![]() 平移。使点
平移。使点![]() 变换为点
变换为点![]() ,点
,点![]() 分 别是
分 别是![]() 的对应点.
的对应点.
(1)请画出平移后的图像![]() (不写画法) ,并直接写出点
(不写画法) ,并直接写出点![]() 的坐标:
的坐标: ![]() ;
;
(2)若![]() 内部一点
内部一点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的对应点
的对应点![]() 的坐标是( ).
的坐标是( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com