
【题目】如图 1,CE 平分∠ACD,AE 平分∠BAC,且∠EAC+∠ACE=90°.
(1)请判断 AB 与 CD 的位置关系,并说明理由;
(2)如图 2,若∠E=90°且 AB 与 CD 的位置关系保持不变,当直角顶点 E 移动时,写出∠BAE 与∠ECD 的数量关系,并说明理由;
(3)如图 3,P 为线段 AC 上一定点,点 Q 为直线 CD 上一动点,且 AB 与 CD 的位置 关系保持不变,当点 Q 在射线 CD 上运动时(不与点 C 重合),∠PQD,∠APQ 与∠ BAC 有何数量关系?写出结论,并说明理由.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,张明同学想测量某铜像的高度,已知铜像(图中![]() )高度比底座(图中
)高度比底座(图中![]() )高度多1米,张明随后用高度为1米的测角仪(图中
)高度多1米,张明随后用高度为1米的测角仪(图中![]() )测得铜像顶端点
)测得铜像顶端点![]() 的仰角β=51°24′,底座顶端点
的仰角β=51°24′,底座顶端点![]() 的仰角
的仰角![]() =26°36′.请你帮助张明算出铜像AB的高度(把铜像和底座近似看在一条直线上它的抽象几何图形如左图).(参考数据:sin26°36′≈0.45, cos26°36′≈0.89,tan26°36′≈0.5,sin51°24′≈0.78,cos51°24′≈0.6,tan51°24′≈1.25)
=26°36′.请你帮助张明算出铜像AB的高度(把铜像和底座近似看在一条直线上它的抽象几何图形如左图).(参考数据:sin26°36′≈0.45, cos26°36′≈0.89,tan26°36′≈0.5,sin51°24′≈0.78,cos51°24′≈0.6,tan51°24′≈1.25)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山地自行车越来越受中学生的喜爱.一网店经营的一个型号山地自行车,今年一月份销售额为30000元,二月份每辆车售价比一月份每辆车售价降价100元,若销售的数量与上一月销售的数量相同,则销售额是27000元.
(1)求二月份每辆车售价是多少元?
(2)为了促销,三月份每辆车售价比二月份每辆车售价降低了10%销售,网店仍可获利35%,求每辆山地自行车的进价是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A,B在数轴上对应的数分别用a,b表示,并且关于x的多项式(a+10)x7+2xb-15﹣4是五次二项式,P,Q是数轴上的两个动点.
(1)a=_____,b=_____;
(2)设点P在数轴上对应的数为x,PA+PB=40,求x的值;
(3)动点P,Q分别从A,B两点同时出发向左运动,点P,Q的运动速度分别为3个单位长度/秒和2个单位长度/秒.点M是线段PQ中点,设运动的时间小于6秒,问6AM+5PB的值是否发生变化?若不变,求其值;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向的B处,求此时轮船所在的B处与灯塔P的距离.(参考数据:![]() ≈2.449,结果保留整数)
≈2.449,结果保留整数)
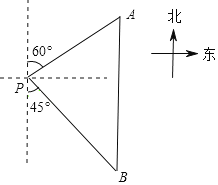
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的边AB、AC为腰分别向外作等腰直角三角形ABD和等腰直角三角形ACE,连接DE.若M为BC中点,MA延长线交DE于点H,
(1) 求证:AH⊥DE.
(2) 若DE=4,AH=3,求△ABM的面积

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家电商场计划用9万元从生产厂家购进50台电视机,已知该厂家生产3种不同型号的电视机,出厂价分别为A种每台1500元,B种每台2100元,C种每台2500元.
(1)若家电商场同时购进两种不同型号的电视机共50台,用去9万元,请你计算一下商场有哪几种进货方案?
(2)若商场销售一台A种电视机可获利150元,销售一台B种电视机可获利200元,销售一台C种电视机可获利250元,在同时购进两种不同型号的电视机方案中,为了使销售时获利最多,应选择哪种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形 ABCD 中,对角线 AC、BD 相交于点 O,过点 O 的两条直线分别交边 AB、CD、AD、BC 于点 E、F、G、H.
(感知)如图①,若四边形 ABCD 是正方形,且 AG=BE=CH=DF,则 S 四边形AEOG= S 正方形 ABCD;
(拓展)如图②,若四边形 ABCD 是矩形,且 S 四边形 AEOG=![]() S 矩形 ABCD,设 AB=a, AD=b,BE=m,求 AG 的长(用含 a、b、m 的代数式表示);
S 矩形 ABCD,设 AB=a, AD=b,BE=m,求 AG 的长(用含 a、b、m 的代数式表示);
(探究)如图③,若四边形 ABCD 是平行四边形,且 AB=3,AD=5,BE=1, 试确定 F、G、H 的位置,使直线 EF、GH 把四边形 ABCD 的面积四等分.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在平面直角坐标系中,直线AB与![]() 轴交于点A(-2,0),与
轴交于点A(-2,0),与![]() 轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线
轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线![]() 上,则
上,则![]() 的值( )
的值( )

A. -4 B. -2 C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com