
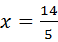 时,△PQR与△CBO一定相似.
时,△PQR与△CBO一定相似.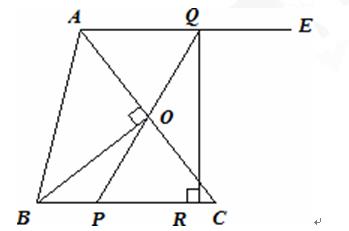
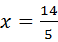 时,
时,

科目:初中数学 来源: 题型:
| A.对角线相等且互相垂直的四边形是正方形 | |
| B.如果两个三角形有两条边和一个角分别对应相等,那么这两个三角形一定全等 | |
| C.角平分线上任意一点到这个角的两边的距离相等 | D.相等的圆周角所对的弧相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:

| A.3 | B.4 |
| C.5 | D.6 |
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(四川攀枝花卷)数学解析版 题型:解答题
(2011•攀枝花)一个不透明的袋子中,装有红黑两种颜色的小球(除颜色不同外其他都相同),其中一个红球,两个分别标有A、B黑球.
(1)小李第一次从口袋中摸出一个球,并且不放回,第二次又从口袋中摸出一个球,则小李两次都摸出黑球的概率是多少?试用树状图或列表法加以说明;
(2)小张第一次从口袋中摸出一个球,摸到红球不放回,摸到黑球放回.第二次又从口袋中摸出一个球,则小张第二次摸到黑球的概率是多少?试用 树状图或列表法加以说明.
树状图或列表法加以说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com