【答案】
分析:(1)将A、B、C三点的坐标代入已知的抛物线的解析式利用待定系数法及其求得a、c的值,配方后即可确定其顶点坐标;
(2)设抛物线对称轴与x轴交点为M,则可得到AM=1,然后根据O′A=OA=2得到O′A=2AM,最后在Rt△OAC中,利用OC和OA的关系列出有关t的方程求得t值即可.
(3)本题需先分两种情况进行讨论,当P是EF上任意一点时,可得PC>PB,从而得出PB≠PA,PB≠PC,PB≠PD,即可求出线段PA、PB、PC、PD不能构成平行四边形.
(4)分假设点P为FG与对称轴交点时,存在一个正数t,使得线段PA、PB、PC、PD能构成一个平行四边形和假设当点P为EH与对称轴交点时,存在一个正数t,使得线段PA、PB、PC、PD能构成一个平行四边形两种情况列出有关的方程求得t值即可.
解答:解:(1)把点A、C的坐标(2,0)、(0,-8t)代入抛物线y=ax
2-6ax+c得,

,解得

,
该抛物线为y=-tx
2+6tx-8t=-t(x-3)
2+t.
∴顶点D坐标为(3,t)
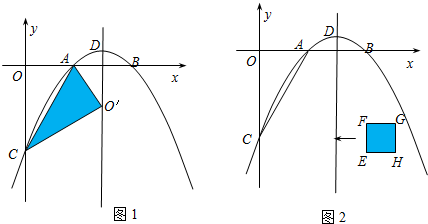
(2)如图1,设抛物线对称轴与x轴交点为M,则AM=1.
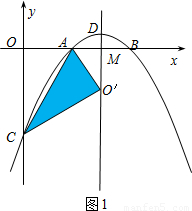
由题意得:O′A=OA=2.
∴O′A=2AM,∴∠O′AM=60°.
∴∠O′AC=∠OAC=60°
∴在Rt△OAC中:
∴OC=
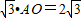
,
即
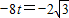
.
∴
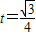
.
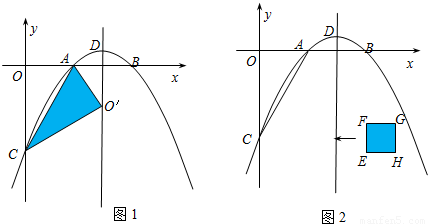
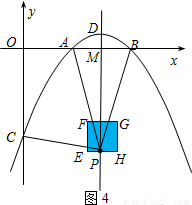
(3)①如图2所示,设点P是边EF上的任意一点
(不与点E、F重合),连接PM.
∵点E(4,-4)、F(4,-3)与点B(4,0)在一直线上,
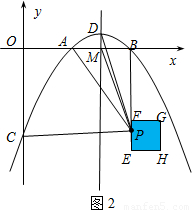
点C在y轴上,
∴PB<4,PC≥4,∴PC>PB.
又PD>PM>PB,PA>PM>PB,
∴PB≠PA,PB≠PC,PB≠PD.
∴此时线段PA、PB、PC、PD不能构成平行四边形.
②设P是边FG上的任意一点(不与点F、G重合),
∵点F的坐标是(4,-3),点G的坐标是(5,-3).
∴FB=3,
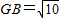
,∴3≤PB≤
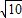
.
∵PC>4,∴PC>PB.
∴PB≠PA,PB≠PC.
∴此时线段PA、PB、PC、PD不能构成平行四边形.
(4)t=
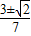
或

或1.
∵已知PA、PB为平行四边形对边,
∴必有PA=PB.
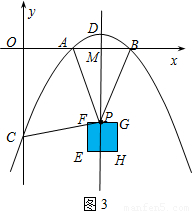
①假设点P为FG与对称轴交点时,存在一个正数t,使得线段PA、PB、PC、PD能构成一个平行四边形.
如图3所示,只有当PC=PD时,线段PA、PB、PC、PD能构成一个平行四边形.
∵点C的坐标是(0,-8t),点D的坐标是(3,t),
又点P的坐标是(3,-3),
∴PC
2=3
2+(-3+8t)
2,PD
2=(3+t)
2.
当PC=PD时,有PC
2=PD
2即 3
2+(-3+8t)
2=(3+t)
2.
整理得7t
2-6t+1=0,
∴解方程得t=
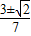
>0满足题意.
②假设当点P为EH与对称轴交点时,存在一个正数t,使得线段PA、PB、PC、PD能构成一个平行四边形.
如图4所示,只有当PC=PD时,线段PA、PB、PC、PD
能构成一个平行四边形.
∵点C的坐标是(0,-8t),点D的坐标是(3,t),
点P的坐标是(3,-4),
∴PC
2=3
2+(-4+8t)
2,PD
2=(4+t)
2.
当PC=PD时,有PC
2=PD
2即 3
2+(-4+8t)
2=(4+t)
2整理得7t
2-8t+1=0,
∴解方程得t=

或1均大于>0满足题意.
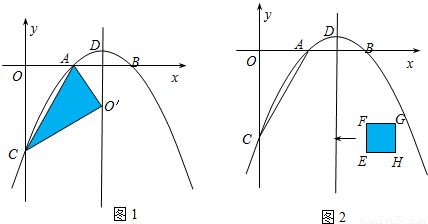
综上所述,满足题意的t=
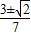
或

或1.
点评:本题主要考查了二次函数的综合问题,在解题时要注意运用数形结合和分类讨论,把二次函数的图象与性质和平行四边形的判定相结合是本题的关键.

 ,解得
,解得  ,
,
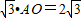 ,
,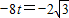 .
.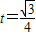 .
. 
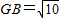 ,∴3≤PB≤
,∴3≤PB≤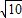 .
.
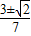 或
或 或1.
或1. 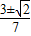 >0满足题意.
>0满足题意.
 或1均大于>0满足题意.
或1均大于>0满足题意.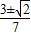 或
或 或1.
或1.