
 的图象交于M、N两点.
的图象交于M、N两点.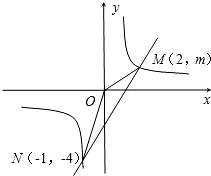
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案科目:初中数学 来源:不详 题型:解答题
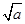 -
- )2≥0,∴a-2
)2≥0,∴a-2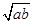 +b≥0,∴a+b≥2
+b≥0,∴a+b≥2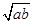 ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.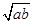 (a、b均为正实数)中,若ab为定值p,则a+b≥2
(a、b均为正实数)中,若ab为定值p,则a+b≥2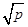 ,只有当a=b时,a+b有最小值2
,只有当a=b时,a+b有最小值2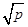 . 根据上述内容,回答下列问题:
. 根据上述内容,回答下列问题: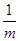 有最小值 ;
有最小值 ; 有最小值 .
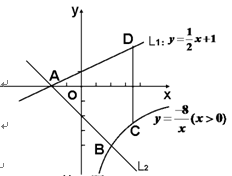
有最小值 . x+1与x轴交于点A,过点A的另一直线L2与双曲线y=
x+1与x轴交于点A,过点A的另一直线L2与双曲线y=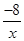
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
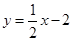 的图象分别交x轴、y轴于A、B,P为AB上一点且PC为△AOB的中位线,PC的延长线交反比例函数
的图象分别交x轴、y轴于A、B,P为AB上一点且PC为△AOB的中位线,PC的延长线交反比例函数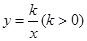 的图象于Q,
的图象于Q,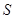 △OCQ=
△OCQ=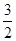
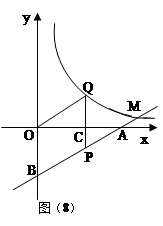
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
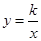 图象上的点,其中x1=1、x2=2、…、xn=n.记T1=x1·y2、T2=x2·y3、…、T2012=x2012·y2013.若T1=
图象上的点,其中x1=1、x2=2、…、xn=n.记T1=x1·y2、T2=x2·y3、…、T2012=x2012·y2013.若T1=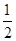 ,则T1·T2·…·T2012=【 】
,则T1·T2·…·T2012=【 】A.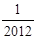 | B.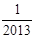 | C.2012 | D.2013 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的图象交于点A(4,m)和B(-8,-2),与y轴交于点C,与x轴交于点D.
的图象交于点A(4,m)和B(-8,-2),与y轴交于点C,与x轴交于点D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com