
分析 (1)根据乘法分配律简便计算;
(2)先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.
解答 解:(1)(-$\frac{1}{6}$+$\frac{3}{4}$-$\frac{5}{12}$)×(-12)
=$\frac{1}{6}$×12-$\frac{3}{4}$×12+$\frac{5}{12}$×12
=2-9+5
=-2;
(2)-22+3×(-1)2016-|-4|×5
=-4+3×1-4×5
=-4+3-20
=-21.
点评 此题考查了有理数的混合运算,进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.规律方法:有理数混合运算的四种运算技巧 1.转化法:一是将除法转化为乘法,二是将乘方转化为乘法,三是在乘除混合运算中,通常将小数转化为分数进行约分计算. 2.凑整法:在加减混合运算中,通常将和为零的两个数,分母相同的两个数,和为整数的两个数,乘积为整数的两个数分别结合为一组求解. 3.分拆法:先将带分数分拆成一个整数与一个真分数的和的形式,然后进行计算. 4.巧用运算律:在计算中巧妙运用加法运算律或乘法运算律往往使计算更简便.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 油电混动汽车 | 普通汽车 | |
| 购买价格(万元) | 17.48 | 15.98 |
| 每百公里燃油成本(元) | 31 | 46 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
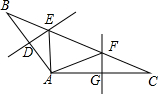 如图,△ABC的周长为30cm,∠BAC=125°,AB+AC=18cm,AB、AC的垂直平分线分别交BC于E、F,与AB、AC分别交于点D、G.
如图,△ABC的周长为30cm,∠BAC=125°,AB+AC=18cm,AB、AC的垂直平分线分别交BC于E、F,与AB、AC分别交于点D、G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com