
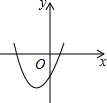
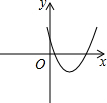
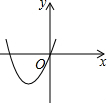
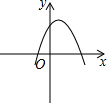
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2013-2014学年山东烟台海阳市九年级上期末数学试卷(解析版) 题型:填空题
二次函数y=ax +bx+c的图像如图所示,则不等式ax
+bx+c的图像如图所示,则不等式ax +bx+c>0的解集是
.
+bx+c>0的解集是
.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年广东省广州市海珠区九年级上学期期末数学试卷(解析版) 题型:解答题
二次函数y=ax²-6ax+c(a>0)的图像抛物线过点C(0,4),设抛物线的顶点为D。

(1)若抛物线经过点(1,-6),求二次函数的解析式;
(2)若a=1时,试判断抛物线与x轴交点的个数;
(3)如图所示A、B是⊙P上两点,AB=8,AP=5。且抛物线过点A(x1,y1),B(x2,y2),并有AD=BD。设⊙P上一动点E(不与A、B重合),且∠AEB为锐角,若<a≤1时,请判断∠AEB与∠ADB的大小关系,并说明理由。
查看答案和解析>>
科目:初中数学 来源:2013-2014学年广东省广州市海珠区九年级上学期期末数学试卷(解析版) 题型:选择题
已知二次函数y=ax²+bx+c(a≠0)的图像如图所示,则下列结论中正确的是( )

A.a>0 B.3是方程ax²+bx+c=0的一个根
C.a+b+c=0 D.当x<1时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏盐城亭湖区九年级下学期第一次调研考试数学试卷(解析版) 题型:解答题
如图11,已知○为坐标原点,∠AOB=30°,∠ABO=90°,且点A的坐标为(2,0).

1.求点B的坐标
2.若二次函数y=ax+bx+c的图象经过A、B、O三点,求此二次函数的解析式;
3.在(2)中的二次函数图象的OB段(不包括点O、B)上,是否存在一点C,使得四边形ABCO的面积最大?若存在,求出这个最大值及此时点C的坐标;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com