
����Ŀ��ͼ1�DZ߳��ֱ�Ϊ4 ![]() ��2�������ȱ�������ֽƬABC��OD��E�������һ��C��O�غϣ���
��2�������ȱ�������ֽƬABC��OD��E�������һ��C��O�غϣ��� 
��1���������̶���ABC������ODE�Ƶ�C˳ʱ����ת30�㣬��õ���ODE������AD��BE��CE���ӳ��߽�AB��F��ͼ2���� ̽������ͼ2�У��߶�BE��AD֮���������Ĵ�С��ϵ����֤����Ľ��ۣ�
��2���ڣ�1���������½���ODE�����߶�CF������CF������ÿ��1����λ���ٶ�ƽ�ƣ�ƽ�ƺ�ġ�CDE��Ϊ��PQR������P���F�غ�ʱֹͣ�˶���ͼ3���� ̽�������PQR�ƶ���ʱ��Ϊx�룬��PQR���ABC�ص����ֵ����Ϊy����y��x֮��ĺ�������ʽ����д�������Ա���x��ȡֵ��Χ��
��3����ͼ1�С�ODE�̶����ѡ�ABC����OE����ƽ�ƣ�ʹ����C����OE���е�G������Ϊ��ABG��Ȼ��ABG�Ƶ�G˳ʱ����ת����BG����DE�ڵ�M����AG����DO�ڵ�N�����BGE=����30�㣼����90�㣩��ͼ4���� ̽������ͼ4�У��߶�ONEM��ֵ�Ƿ�����ı仯���仯�����û�б仯���������ONEM��ֵ������б仯������˵����
���𰸡�
��1���⣺BE=AD��
֤������ͼ2���ߡ�ABC���DCE�ǵȱ������Σ�
���ACB=��DCE=60�㣬CA=CB��CE=CD��
���BCE=��ACD��
�ڡ�BCE���ACD�У�
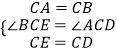 ��
��
���BCE�ա�ACD��SAS����
��BE=AD
��2���⣺��ͼ3���ڡ�CQT��

�ߡ�TCQ=30���RQP=60�㣬
���QTC=30�㣬
���QTC=��TCQ��
��QT=QC=x��
��RT=2��x��
�ߡ�RTS+��R=90��
���RST=90��
��y= ![]() ��22��
��22�� ![]() ��2��x��2=��
��2��x��2=�� ![]() ��2��x��2+
��2��x��2+ ![]() ��0��x��2��
��0��x��2��
��3���⣺ONEM��ֵ���䣬
����Ϊ����ͼ4���ߡ�AGB=60�㣬
���MGE+��NGO=120�㣬
�ߡ�GNO+��NGO=120�㣬
���MGE=��GNO��
�ߡ�E=��O��
���EMG�ס�OGN��
�� ![]() =
= ![]() ��
��
��ONEM=OGEG=1��
����������1����ͨ��֤������BEC��ACDȫ�����ó�BE=AD����2�������غϲ��ֵ������ֱ���������˿��á�RPQ�������ȥ��RST���������ã�S��TΪRP��RQ��AC�Ľ��㣩����PRQ���������ã��ؼ��ǡ�RST�������������RST�У����ڡ�RTS=��CTQ=60�㩁��TCQ=30�㣬����R=60�㣬��ˡ�RST��ֱ�������Σ�ֻ�����RS��ST�ij����ɣ������Ѿ�����ˡ�QTC=��QCT=30�㣬���RT=RQ��QT=RQ��QC=3��x��Ȼ����ݡ�RTS������ǵĶ��������ɵó�RS��ST�ij��������ɵó�y��x�ĺ�����ϵʽ����3�������ͨ��֤��GEM�͡�NGO��������⣮
�����㾫����������Ĺؼ������������������ε��ж������ʵ����֪ʶ���������������ε�һ�ж�Ӧ�߶�(��Ӧ�ߡ���Ӧ���ߡ���Ӧ��ƽ���ߡ����Բ�뾶������Բ�뾶�ȣ��ıȵ������Ʊȣ������������ܳ��ıȵ������Ʊȣ���������������ıȵ������Ʊȵ�ƽ����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ABCD�У��Խ���AC��BD���ڵ�O����Rt��PMN�У���MPN=90�㣮
��1����ͼ1������P���O�غ���PM��AD��PN��AB���ֱ�AD��AB�ڵ�E��F����ֱ��д��PE��PF��������ϵ��
��2����ͼ1�е�Rt��PMN�Ƶ�O˳ʱ����ת�ǶȦ���0�㣼����45�㣩��
����ͼ2������ת�����У�1���еĽ�����Ȼ����������������֤����������������˵�����ɣ�
����ͼ2������ת�����У�����DOM=15��ʱ������EF���������εı߳�Ϊ2����ֱ��д���߶�EF�ij���
����ͼ3����ת����Rt��PMN�Ķ���P���߶�OB���ƶ��������O��B�غϣ�����BD=3BPʱ�������ʱPE��PF��������ϵ��������֤������BD=mBPʱ����ֱ��д��PE��PF��������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�����س���ѧ������������ѡ��Ŀ������������г���ѧ���������ȡ�в���ѧ������ѡ��Ŀ����ͳ�ƣ�����������ͳ��ͼ��Ƶ���ֲ�ֱ��ͼ�������ͼ����Ϣ���ش��������⣺ 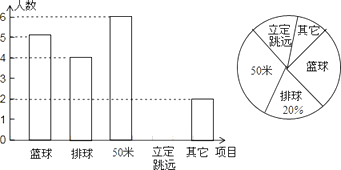
��1�����ε��鹲��ȡ����ѧ����
��2���˴ε��鱨������Ŀ������ռ������ٷ���������������Զ����������
��3������ͳ��ͼ��50�ײ�������Ӧ��Բ�ĽǵĶ�������
��4�����й��г���ѧ��3000�������������ж�����ѧ��ѡ��������Ŀ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ1,�����������Σ�ÿ���Ƕ���![]() ����һ�������غϷ���,��
����һ�������غϷ���,��![]() ����
����![]() �Ķ���;
�Ķ���;
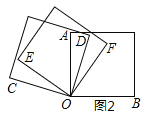
��2����ͼ2,�����������ε�һ�������غϷ��ã���![]() ,��
,��![]() �Ķ���;
�Ķ���;
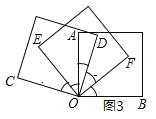
��3����ͼ3,�����������ε�һ�������غϷ���,��![]() ƽ��
ƽ��![]() ,��ô
,��ô![]() ƽ��
ƽ��![]() ��?Ϊʲô?
��?Ϊʲô?

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ѧУ���꼶ѧ������������ǰ�����ڻ���ѵ���Լ��Ŀ�����Ŀ����ǿ�ͱ���ͬѧ���Լ�ѡ���������Ŀ��������һ�ε���ͳ�ƣ���������ͨ���ռ����ݺ��Ƶ�������������ͳ��ͼ���������ͼ���ṩ����Ϣ������������⣺ 
��1���ð����ѧ����
��2����ȫ����ͳ��ͼ��
��3��������ͳ��ͼ�У�������������Ӧ��Բ�ĽǶ���Ϊ��
��4����ȫУ��360��ѧ����������ȫУ�����������ֵ�ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪���κ���y=ax2+bx+c��a��0����ͼ��Ķ���P�ĺ�������4��ͼ��x���ڵ�A��m��0���͵�B����m��4����ôAB�ij��ǣ� �� 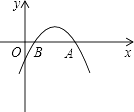
A.4+m
B.m
C.2m��8
D.8��2m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y1=ax2+bx+c��a��0��ͼ���һ���֣������ߵĶ�������A��1��3������x���һ������B��4��0����ֱ��y2=mx+n��m��0���������߽���A��B���㣬���н��ۣ� ��2a+b=0��
��abc��0��
�۷���ax2+bx+c=3��������ȵ�ʵ������
����������x�����һ�������ǣ���1��0����
�ݵ�1��x��4ʱ����y2��y1 ��
������ȷ���ǣ� ��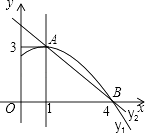
A.�٢ڢ�
B.�٢ۢ�
C.�٢ۢ�
D.�ڢܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ������Ϊ4Ԫ������Ʒ������ÿ��5Ԫ�ļ۸����ۣ�ÿ��������3���������ÿ��6Ԫ�ļ۸����ۣ�ÿ��������2������ٶ�ÿ�����ۼ���y��������۸�x��Ԫ/����֮������һ�κ�����ϵ��
��1������y��x֮��ĺ�����ϵʽ��
��2�������ۼ۸�Ϊ����ʱ������ʹÿ�µ��������ÿ�µ���������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=��x2+2x+3��y�ύ�ڵ�C����D��0��1������P���������ϵĶ��㣮����PCD����CDΪ�ĵ��������Σ����P������Ϊ �� 
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com