
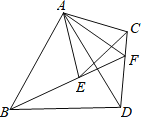
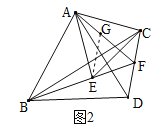
【题目】如图,![]() ,分别以AB、AC为边作等边三角形ABD与等边三角形ACE,连接BE、CD,BE的延长线与CD交于点F,连接AF,有以下四个结论:①
,分别以AB、AC为边作等边三角形ABD与等边三角形ACE,连接BE、CD,BE的延长线与CD交于点F,连接AF,有以下四个结论:①![]() ;②FA平分
;②FA平分![]() ;③
;③![]() ;④
;④![]() .其中一定正确的结论有( )
.其中一定正确的结论有( )
A.1B.2C.3D.4
【答案】C
【解析】
根据等边三角形的性质证出△BAE≌△DAC,可得BE=CD,从而得出①正确;
过A作AM⊥BF于M,过A作AN⊥DC于N,由△BAE≌△DAC得出∠BEA=∠ACD,由等角的补角相等得出∠AEM=∠CAN,由AAS可证△AME≌△ANC,得到AM=AN,由角平分线的判定定理得到FA平分∠EFC,从而得出②正确;
在FA上截取FG,使FG=FE,根据全等三角形的判定与性质得出△AGE≌△CFE,可得AG=CF,即可求得AF=CF+EF,从而得出④正确;
根据CF+EF=AF,CF+DF=CD,得出CD≠AF,从而得出FE≠FD,即可得出③错误.
∵△ABD和△ACE是等边三角形,
∴∠BAD=∠EAC=60°,AE=AC=EC.
∵∠BAE+∠DAE=60°,∠CAD+∠DAE=60°,
∴∠BAE=∠DAC,
在△BAE和△DAC中,
∵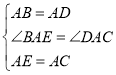 ,
,
∴△BAE≌△DAC(SAS),
∴BE=CD,①正确;
过A作AM⊥BF于M,过A作AN⊥DC于N,如图1.
∵△BAE≌△DAC,
∴∠BEA=∠ACD,
∴∠AEM=∠ACN.
∵AM⊥BF,AN⊥DC,
∴∠AME=∠ANC.
在△AME和△ANC中,∵∠AEM=∠CAN,∠AME=∠ANC,AE=AC,
∴△AME≌△ANC,
∴AM=AN.
∵AM⊥BF,AN⊥DC,AM=AN,FA平分∠EFC,②正确;
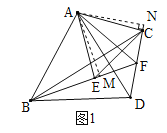
在FA上截取FG,使FG=FE,如图2.
∵∠BEA=∠ACD,∠BEA+∠AEF=180°,
∴∠AEF+∠ACD=180°,
∴∠EAC+∠EFC=180°.
∵∠EAC=60°,
∴∠EFC=120°.
∵FA平分∠EFC,
∴∠EFA=∠CFA=60°.
∵EF=FG,∠EFA=60°,
∴△EFG是等边三角形,
∴EF=EG.
∵∠AEG+∠CEG=60°,∠CEG+∠CEF=60°,
∴∠AEG=∠CEF,
在△AGE和△CFE中,
∵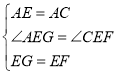 ,
,
∴△AGE≌△CFE(SAS),
∴AG=CF.
∵AF=AG+FG,
∴AF=CF+EF,④正确;
∵CF+EF=AF,CF+DF=CD,CD≠AF,
∴FE≠FD,③错误,
∴正确的结论有3个.
故选C.


科目:初中数学 来源: 题型:
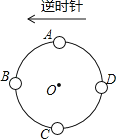
【题目】如图,一枚棋子放在⊙O上的点A处,通过摸球来确定该棋子的走法.
其规则如下:在一只不透明的口袋中,装有3个标号分别为1,2,3的相同小球.充分搅匀后从中随机摸出1个,记下标号后放回袋中并搅匀,再从中随机摸出1个,若摸出的两个小球标号之积是m,就沿着圆周按逆时针方向走m步(例如:m=1,则A﹣B;若m=6,则A﹣B﹣C﹣D﹣A﹣B﹣C).用列表或树状图,分别求出棋子走到A、B、C、D点的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
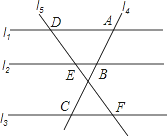
【题目】如图,直线l1、l2、l3分别交直线l4于点A、B、C,交直线l5于点D、E、F,且l1∥l2∥l3 , 已知EF:DF=5:8,AC=24.
(1)求AB的长;
(2)当AD=4,BE=1时,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD=AE,添加下列条件仍无法证明△ABE≌△ACD的是 ( )

A. AB=AC B. ∠ADC=∠AEB C. ∠B=∠C D. BE=CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面内容:我们已经学习了《二次根式》和《乘法公式》,聪明的你可以发现:
当![]() ,
,![]() 时,
时,
![]() ,
,
![]() ,当且仅当
,当且仅当![]() 时取等号.
时取等号.
请利用上述结论解决以下问题:
(1)当![]() 时,
时,![]() 的最小值为__________.
的最小值为__________.
(2)当![]() 时,求
时,求![]() 的最小值.
的最小值.
(3)请解答以下问题:
如图所示,某园艺公司准备围建一个矩形花圃,其中一边靠墙(墙足够长),另外三边用篱笆围成,设垂直于墙的一边长为![]() 米.若要围成面积为200平方米的花圃,需要用的篱笆最少是__________米.
米.若要围成面积为200平方米的花圃,需要用的篱笆最少是__________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
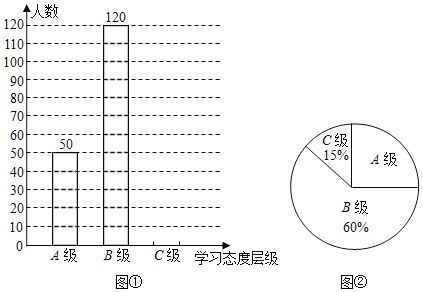
【题目】我校对八年级学生的学习态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了多少名学生;
(2)通过计算达到C级的有多少人?并补全条形图.
(3)根据抽样调查结果,请你估计我市近80000名八年级学生中大约有多少名学生学习态度达标(达标指的是学习兴趣达到A级和B级)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点![]() 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为
周长的最小值为![]()
![]()

A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com