练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在中，为的内切圆，点是斜边的中点，则（    ）

    A．       　B．    　C．    　　D．2

    Ｄ

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

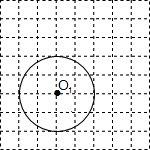    精英家教网如图，在边长为1的小正方形组成的网格中，半径为2的⊙O1的圆心O1在格点上，将一个与⊙O1重合的等圆向右平移2个单位，再向上平移2个单位得到⊙O2．则⊙O2与⊙O1的位置关系是（　　）
    A、内切B、外切C、相交D、外离

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•廊坊一模）圆的滚动问题探索：
    （1）如图1，一个半径为r的圆沿直线方向从A地滚动到B地，若AB的长为m，则该圆在滚动过程中自转了
    m
    2πr
    m
    2πr
    圈．（用含的式子表示）
    试验：
    现有两个半径相等的圆（如图5），将⊙O2固定，⊙O1沿定圆的周围滚动，滚动时两圆保持相外切的位置关系．当⊙O1沿⊙O2周围滚动一周回到原来的位置时，⊙O1自转了2圈，而⊙O1的圆心运动的线路也是一个圆，而这个圆的周长恰好是⊙O1的周长的2倍．
    （2）如图2，⊙O1的半径为r，⊙O2的半径为R（R＞r），现将⊙O2固定，让，⊙O1沿⊙O2的周围滚动，滚动时两圆保持相外切的位置关系．当⊙O1沿⊙O2沿周围滚动一周回到原来的位置时，⊙O1自转了
    R+r
    r
    R+r
    r
    圈；

    （3）如图3，⊙O1，和⊙O2内切，⊙O1的半径为r，⊙O2的半径为R（R＞r），现将⊙O2固定，让，⊙O1沿⊙O2的边缘滚动，动时两圆保持相内切的位置关系．当⊙O1沿⊙O2边缘滚动一圈回到原来的位置时，⊙O1自转了
    R-r
    r
    R-r
    r
    圈．
    解决问题：
    如图4，一个等边三角形与它的一边相切的圆的周长相等，当此圆按箭头方向从某一位置沿等边三角形的三边作无滑动滚动，直至回到原来的位置时，该圆自转了多少圈？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （1998•四川）已知：如图，在以O 为圆心的两个同心圆中，大圆O的内接四边形ABCD的边AB切小圆O于点P，两条对角线AC、BD相交于点Q，AQ和AD的长是方程x2-7x+12=0的两根，小圆O的半径等于CD长的一半，AK是大圆的直径．
    （1）求证：∠BAK=∠CAD；
    （2）求sin∠ADQ的值．

    查看答案和解析>>

    科目：初中数学 来源：2010-2011学年南京市考数学一模试卷 题型：填空题

    如图，在边长为2的正方形ABCD中，分别以各顶点为圆心在正方形内作四条圆弧，使它们所在的圆外切于点E，F，G，H．则图中阴影部分外围的周长是        （结果保留）．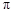

     

    查看答案和解析>>

    科目：初中数学 来源：2010年福建省宁德市中考数学试卷（解析版） 题型：选择题

    （2010•宁德）如图，在7×4的方格（每个方格的边长为1个单位长）中，⊙A的半径为1，⊙B的半径为2，将⊙A由图示位置向右平移1个单位长后，⊙A与静止的⊙B的位置关系是（ ）

    A．内含
    B．内切
    C．相交
    D．外切

    查看答案和解析>>

    同步练习册答案