
分析 (1)若设购买甲种树苗x株,则购买乙种树苗是(6000-x)株,由甲、乙树苗单株价格,根据购买这批树苗的钱不超过4200元,得到关于x的不等式,解不等式从而得到应该如何选购树苗.
(2)根据成活率列出关于x的不等式,得到x的取值范围,再列出购买树苗总费用的函数关系,根据一次函数的性质,确定购买甲种树苗的株数.
解答 解:(1)设购买甲种树苗x株,购买乙种树苗(6000-x)株,
由题意得:0.5x+0.8(6000-x)≤4200
解这个不等式,得:x≥2000
即购买甲种树苗应不少于2000株.
(2)设购买树苗的总费用为y,则y=0.5x+0.8(6000-x)
=-0.3x+4800
由题意,有$\frac{90}{100}x+\frac{95}{100}(6000-x)≥\frac{93}{100}×6000$
解得:x≤2400
在y=-0.3x+4800中
∵-0.3<0,∴y随x的增大而减少
∴当x=2400时,y最小=4080.
即购买甲种树苗2400株,乙种树苗3600株时,总费用最低.
点评 本题考查了一元一次不等式的应用及一次函数在生活中的应用.能根据购买树苗总钱数、树苗成活率和一次函数的性质,列出不等式和函数关系式,是确定如何选购树苗的关键.


科目:初中数学 来源: 题型:解答题
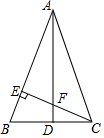 如图,在△ABC中,AB=AC,BD=CD,CE⊥AB于E,BE=2,BC=6.
如图,在△ABC中,AB=AC,BD=CD,CE⊥AB于E,BE=2,BC=6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
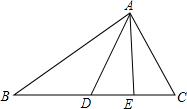 如图,已知在△ABC中,∠CAE=∠B,点E是CD的中点,若AD平分∠BAE.
如图,已知在△ABC中,∠CAE=∠B,点E是CD的中点,若AD平分∠BAE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第一次 | 第二次 | |
| 甲种车辆数单位(辆) | 2 | 5 |
| 乙种车辆数单位(辆) | 3 | 6 |
| 累计运货数单位(吨) | 15.5 | 35 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
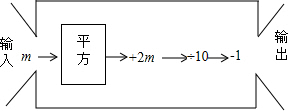
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com