
【题目】阅读下面材料:
小腾遇到这样一个问题:如图1,在![]() 中,点
中,点![]() 在线段
在线段![]() 上.
上.![]() ,
,![]() ,
,![]() ,
,![]() .求
.求![]() 的长.
的长.
小腾发现,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,通过构造
,通过构造![]() ,经过推理和计算能够使问题得到解决(如图2).
,经过推理和计算能够使问题得到解决(如图2).

发现:![]() 的度数为 ,
的度数为 ,![]() 的长为
的长为
探究:参考小腾思考问题的方法,解决问题:
如图3,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,求
,求![]() ,
,![]() 的长.
的长.
【答案】发现:∠ACE的度数为75°,AC的长为3;探究:![]() ,
,![]()
【解析】
发现:根据平行线的性质得到∠E=∠BAD=75°,根据三角形内角和定理即可得出![]() ,证明△ABD∽△DCE,根据相似三角形的性质得出AC的长;
,证明△ABD∽△DCE,根据相似三角形的性质得出AC的长;
探究:过点D作DF⊥AC于点F,证明△ABE∽△FDE,根据相似三角形的性质求出EF、AF,根据正切的概念求出DF,根据勾股定理计算即可.
发现:∵CE∥AB,
∴∠E=∠BAD=75°,
∴∠ACE=180°-∠CAD-∠E=180°-75°-30°=75°,
∵∠E=75°,∴∠ACE=∠E,
∴AC=AE,
∵CE∥AB,BD=2DC,
∴△ABD∽△DCE,
∴![]()
∴AD=2DE,
∴DE=1,∴AE=3,
∴AC=3;∴AD=2DE,
∵AE=AD+DE=3,
∴AC=AE=3;
故答案为:75,3
探究:过点D作DF⊥AC于F,如图

∵ ∠BAC=90°,
∴ AB∥DF,∴ △ABE∽△FDE.
∴ ![]()
∴EF=1 , AB=2DF.
∴AF=3
在Rt△ACD中,∠CAD=30°
设DF=x,则AD=2x,
由勾股定理得![]() ,解得
,解得![]() ,∴
,∴![]()
∵ 在△ACD中,∠CAD=30°,∠ADC=75°,
∴ ∠ACD=75°,∴ AC=AD
∵AD=2DF ,AB=2DF
∴AD=AB
∴AB=AC
![]()


科目:初中数学 来源: 题型:
【题目】六一前夕某幼儿园园长到厂家选购A、B两种品牌的儿童服装每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍,求A、B两种品牌服装每套进价分别为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
材料一:所有正整数在进行某种规定步骤的运算后,会得到一个恒定不变的数,我们把这个恒定不变的数叫做稳定数.规定求三位数的稳定数的运算步骤是:任意三位数A=![]() (百位与个位不相同),将这个数逆置后得A1=
(百位与个位不相同),将这个数逆置后得A1=![]() ,A与A1中较大的数减去较小的数得到一个数B,再将B进行一次逆置得B1(若B为两位数则交换十位与个位逆置),将B1与B相加得C,C就是该三位数A的稳定数,记作
,A与A1中较大的数减去较小的数得到一个数B,再将B进行一次逆置得B1(若B为两位数则交换十位与个位逆置),将B1与B相加得C,C就是该三位数A的稳定数,记作![]() .
.
材料二:当两个三位数的稳定数相同时,这两个三位数的百位数字与个位数字之差的绝对值或者都大于1,或者都等于1.
(1)求352的稳定数是 ;百位与个位相差2的三位数,它的稳定数是 .
(2)现有S=301+10p,T=100m+40+n(1≤p≤9,1≤m≤9,1≤n≤9,p,m,n均是整数),其中T是偶数,若![]() ,3p+m+n=20,|p-n|=1,
,3p+m+n=20,|p-n|=1,![]() ,请求出
,请求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过
经过![]() 点,直线
点,直线![]() 是抛物线的对称轴.
是抛物线的对称轴.
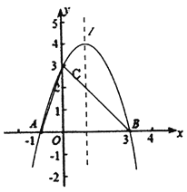
(1)求抛物线的函数关系式;
(2)在直线![]() 上确定一点
上确定一点![]() ,使
,使![]() 的周长最小,求出点
的周长最小,求出点![]() 的坐标;
的坐标;
(3)若点![]() 是抛物线上一动点,当
是抛物线上一动点,当![]() 时,请直接写出点
时,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点P是BC边上一动点,连结AP,AP的垂直平分线交BD于点G,交 AP于点E,在P点由B点到C点的运动过程中,∠APG的大小变化情况是( )
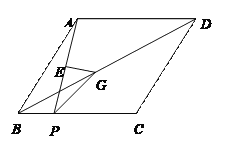
A. 变大 B. 先变大后变小 C. 先变小后变大 D. 不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察如图,填表后再回答问题:
(1)在横线上填入正确的数:
![]() 的个数:8,______ ,24
的个数:8,______ ,24![]()
★的个数:1,4,______ ![]()
(2)试求第6个图形中“![]() ”的个数和“
”的个数和“![]() ”的个数?
”的个数?
(3)试求第108个图形中“![]() ”的个数与“
”的个数与“![]() ”的个数之差?
”的个数之差?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校小伟同学酷爱健身,一天去爬山锻炼,在出发点C处测得山顶部A的仰角为30度,在爬山过程中,每一段平路(CD、EF、GH)与水平线平行,每一段上坡路(DE、FG、HA)与水平线的夹角都是45度,在山的另一边有一点B(B、C、D同一水平线上),斜坡AB的坡度为2:1,且AB长为900![]() ,其中小伟走平路的速度为65.7米/分,走上坡路的速度为42.3米/分.则小伟从C出发到坡顶A的时间为( )(图中所有点在同一平面内
,其中小伟走平路的速度为65.7米/分,走上坡路的速度为42.3米/分.则小伟从C出发到坡顶A的时间为( )(图中所有点在同一平面内![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
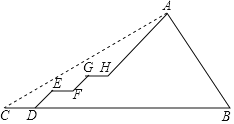
A.60分钟B.70分钟C.80分钟D.90分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的盒子中有2枚黑棋,x枚白棋,这些棋子除颜色外无其他差别,现从盒中随机摸出一枚棋子(不放回),再随机摸出一枚棋子.
(1)若“摸出两枚棋子的颜色都是白色”是不可能事件,请写出符合条件的一个x值 ;
(2)当x=2时,“摸出两枚棋子的颜色相同”与“摸出两枚棋子的颜色不同”的概率相等吗?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com