
【题目】甲口袋中有2个白球、1个红球,乙口袋中有1个白球、1个红球,这些球除颜色外无其他差别.分别从每个口袋中随机摸出1个球.
(1)求摸出的2个球都是白球的概率.
(2)请比较①摸出的2个球颜色相同②摸出的2个球中至少有1个白球,这两种情况哪个概率大,请说明理由
【答案】(1)摸出的2个球都是白球的概率为![]() ;(2)概率最大的是摸岀的2个球中至少有1个白球.理由见解析.
;(2)概率最大的是摸岀的2个球中至少有1个白球.理由见解析.
【解析】
(1)先画树状图展示所以6种等可能的结果,其中摸出的2个球都是白球的有2种结果,然后根据概率定义求解.
(2)根据树状图可知:共有6种等可能的结果,其中摸出的2个球颜色相同的有3种结果,摸出的2个球中至少有1个白球的有5种结果,根据概率公式分别计算出各自的概率,再比较大小即可.
(1)画树状图如下:
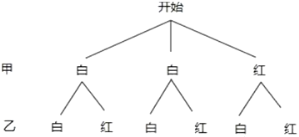
由树状图知,共有6种等可能结果,其中摸出的2个球都是白球的有2种结果,
所以摸出的2个球都是白球的概率为![]() ;
;
(2)∵摸出的2个球颜色相同概率为![]() 、
、
摸出的2个球中至少有1个白球的概率为![]() ,
,
∴概率最大的是摸岀的2个球中至少有1个白球.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=﹣4x2﹣8mx﹣m2+2m的顶点p.
(1)点p的坐标为 (含m的式子表示)
(2)当﹣1≤x≤1时,y的最大值为5,则m的值为多少;
(3)若抛物线与x轴(不包括x轴上的点)所围成的封闭区域只含有1个整数点,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过点A(-3,2),B(0,-2)其对称轴为直线x=![]() ,C(0,
,C(0, ![]() )为y轴上一点,直线AC与抛物线交于另一点D,
)为y轴上一点,直线AC与抛物线交于另一点D,

(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点F使△ADF是直角三角形,如果存在,求出点F的坐标,如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( )

A.5 B.6 C.2![]() D.3
D.3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
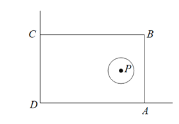
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用26m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设BC=x m.
(1)若矩形花园ABCD的面积为165m2,求 x的值;
(2)若在P处有一棵树,树中心P与墙CD,AD的距离分别是13m和6m,要将这棵树围在花园内(考虑到树以后的生长,篱笆围矩形ABCD时,需将以P为圆心,1为半径的圆形区域围在内),求矩形花园ABCD面积S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小芸设计的“过圆外一点作已知圆的切线”的尺规作图过程.
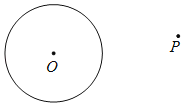
已知:⊙O及⊙O外一点P.
求作:⊙O的一条切线,使这条切线经过点P.
作法:①连接OP,作OP的垂直平分线l,交OP于点A;
②以A为圆心,AO为半径作圆,交⊙O于点M;
③作直线PM,则直线PM即为⊙O的切线.
根据小芸设计的尺规作图过程,
(1)用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1,3.与y轴负半轴交于点C,在下面五个结论中:①2a-b=0;②a+b+c>0;③c=-3a;④只有当a= ![]() 时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a值可以有三个.其中正确的结论是( )
时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a值可以有三个.其中正确的结论是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
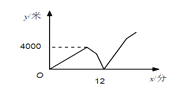
【题目】某公司快递员甲匀速骑车前往某小区送物件,出发几分钟后,快递员乙发现甲的手机落在公司,无法联系,于是乙匀速骑车去追赶甲.乙刚出发2分钟时,甲也发现自己手机落在公司,立刻按原路原速骑车回公司,2分钟后甲遇到乙,乙把手机给甲后立即原路原速返回公司,甲继续原路原速赶往某小区送物件,甲乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示(乙给甲手机的时间忽略不计).则乙回到公司时,甲距公司的路程是______米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xoy中, 一块含60°角的三角板作如图摆放,斜边 AB在x轴上,直角顶点C在y轴正半轴上,已知点A(-1,0).

(1)请直接写出点B、C的坐标:B( , )、C( , );并求经过A、B、C三点的抛物
线解析式;
(2)现有与上述三角板完全一样的三角板DEF(其中∠EDF=90°,∠DEF=60°),把顶点E放在线段
AB上(点E是不与A、B两点重合的动点),并使ED所在直线经过点C. 此时,EF所在直线与(1)中的抛物线交于第一象限的点M.
①设AE=x,当x为何值时,△OCE∽△OBC;
②在①的条件下探究:抛物线的对称轴上是否存在点P使△PEM是等腰三角形,若存在,请求点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com