
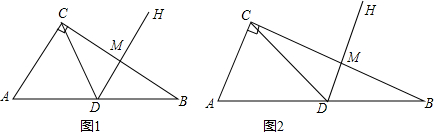
分析 (1)由三角形内角和定理求出∠A的度数,根据D为直角三角形斜边上的中点,得到CD=AD,利用等边对等角及内角和定理得到∠ADC=60°,利用等边三角形的判定方法判断即可得证;
(2)①由D为斜边上的中点,利用直角三角形斜边上的中线等于斜边的一半确定出AC=CD=AD,利用等边对等角得到一对角相等,再由已知角相等,等量代换得到一对内错角相等,确定出DH与AC平行,确定出DM为三角形ABC中位线,利用中位线定理判断即可求出DM的长;
②分三种情况考虑:当MN=DN;当MN=DM;当DN=DM,分别求出MP的长即可.
解答 (1)证明:∵∠B=30°,∠ACB=90°,
∴∠A=60°,
由题意可得D是直角三角形斜边A边上的中点,
∴CD=AD,
∴∠ACD=∠A=60°,
∴∠ADC=60°,
∴△ACD为等边三角形;
(2)解:①∵点D是直角三角形斜边AB上的中点,
∴AC=CD=AD,
∴∠ACD=∠A,
∵∠CDH=∠A,
∴∠ACD=∠CDH,
∴DH∥AC,
∴DM为△ABC的中位线,
∴DM=$\frac{1}{2}$AC=5;
②分三种情况考虑:
(i)当MN=DN时,如图1所示,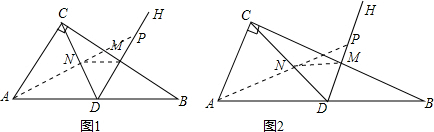 由①得:AD=CD,∠A=∠ACD=∠CDH,DM=5,
由①得:AD=CD,∠A=∠ACD=∠CDH,DM=5,
∵MN=DN,
∴∠CDN=∠DMN=∠A=∠ACD,
∴△ADC∽△DNM,
∴$\frac{DN}{AD}$=$\frac{DM}{AC}$,即$\frac{DN}{13}$=$\frac{5}{10}$,
解得:DN=$\frac{13}{2}$=$\frac{1}{2}$CD,
∴CN=DN,
∵DH∥AC,
∴△ACN≌△PDN,
∴PD=AC=10,
∴MP=PD-DM=10-5=5;
(ii)当MN=DM=5时,如图2所示,则有∠MND=∠MDN=∠ACD=∠A,
∴△ADC∽△MDN,
∴$\frac{DN}{AC}$=$\frac{DM}{AD}$,即$\frac{DN}{10}$=$\frac{5}{13}$,
解得:DN=$\frac{50}{13}$,
∴CN=13-$\frac{50}{13}$=$\frac{119}{13}$,
∵△ACN∽△PDN,
∴$\frac{PD}{AC}$=$\frac{DN}{CN}$,即$\frac{PD}{10}$=$\frac{\frac{50}{13}}{\frac{119}{13}}$,
解得:PD=$\frac{500}{119}$,
则MP=DM-PD=5-$\frac{500}{119}$=$\frac{95}{119}$;
(iii)当DN=DM时,如图2所示,则有DN=5,CN=13-5=8,
∵△ACN∽△PDN,
∴$\frac{PD}{AC}$=$\frac{DN}{CN}$,即$\frac{PD}{10}$=$\frac{5}{8}$,
解得:PD=$\frac{25}{4}$,
则MP=PD-DM=$\frac{5}{4}$.
点评 此题属于三角形综合题,涉及的知识有:相似三角形的判定与性质,直角三角形斜边上的中线性质,等腰三角形的判定与性质,以及平行线的判定与性质,熟练掌握相似三角形的判定与性质是解本题的关键.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{8\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 [实际情境]
[实际情境]查看答案和解析>>
科目:初中数学 来源: 题型:解答题
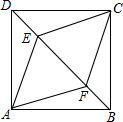 正方形ABCD中,点E,F是对角线BD上的两点,且DE=BF.
正方形ABCD中,点E,F是对角线BD上的两点,且DE=BF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在正方形ABCD中,AB=$\sqrt{2}$,点P为边AB上一动点(不与A、B重合),过A、P在正方形内部作正方形APEF,交边AD于F点,连接DE、EC,当△CDE为等腰三角形时,AP=$\sqrt{2}$-1或$\frac{\sqrt{2}}{2}$.
如图,在正方形ABCD中,AB=$\sqrt{2}$,点P为边AB上一动点(不与A、B重合),过A、P在正方形内部作正方形APEF,交边AD于F点,连接DE、EC,当△CDE为等腰三角形时,AP=$\sqrt{2}$-1或$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{16}$=±4 | B. | 100${\;}^{-\frac{1}{2}}$=-10 | C. | $\root{4}{(-3)^{4}}$=-3 | D. | |$\sqrt{8}$-3|=3-$\sqrt{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com