
”¾ĢāÄæ”æĒé¾³¹Ū²ģ£ŗ

ČēĶ¼1£¬”÷ABCÖŠ£¬AB=AC£¬”ĻBAC=45”ć£¬CD”ĶAB£¬AE”ĶBC£¬“¹×ć·Ö±šĪŖD”¢E£¬CDÓėAE½»ÓŚµćF£®
¢ŁŠ“³öĶ¼1ÖŠĖłÓŠµÄČ«µČČż½ĒŠĪ £»
¢ŚĻ߶ĪAFÓėĻ߶ĪCEµÄŹżĮæ¹ŲĻµŹĒ £®
ĪŹĢāĢ½¾æ£ŗ
ČēĶ¼2£¬”÷ABCÖŠ£¬”ĻBAC=45”ć£¬AB=BC£¬ADĘ½·Ö”ĻBAC£¬AD”ĶCD£¬“¹×ćĪŖD£¬ADÓėBC½»ÓŚµćE£®
ĒóÖ¤£ŗAE=2CD£®
ĶŲÕ¹ŃÓÉģ£ŗ
ČēĶ¼3£¬”÷ABCÖŠ£¬”ĻBAC=45”ć£¬AB=BC£¬µćDŌŚACÉĻ£¬”ĻEDC=![]() ”ĻBAC£¬DE”ĶCE£¬“¹×ćĪŖE£¬DEÓėBC½»ÓŚµćF£®ĒóÖ¤£ŗDF=2CE£®
”ĻBAC£¬DE”ĶCE£¬“¹×ćĪŖE£¬DEÓėBC½»ÓŚµćF£®ĒóÖ¤£ŗDF=2CE£®
ŅŖĒó£ŗĒėÄ抓³öøØÖśĻßµÄ×÷·Ø£¬²¢ŌŚĶ¼3ÖŠ»³öøØÖśĻߣ¬²»ŠčŅŖÖ¤Ć÷£®
”¾“š°ø”æ1£®¢Ł”÷ABE”Õ”÷ACE£¬”÷ADF”Õ”÷CDB£»¢ŚAF=2CE£®¼ū½āĪö£»2.¼ū½āĪö£»3.¼ū½āĪö
”¾½āĪö”æ
Ēé¾³¹Ū²ģ£ŗ¢ŁÓÉČ«µČČż½ĒŠĪµÄÅŠ¶Ø·½·ØČŻŅ×µĆ³ö½į¹ū£»
¢ŚÓÉČ«µČČż½ĒŠĪµÄŠŌÖŹ¼“æÉµĆ³ö½įĀŪ£»
ĪŹĢāĢ½¾æ£ŗŃÓ³¤AB”¢CD½»ÓŚµćG£¬ÓÉASAÖ¤Ć÷”÷ADC”Õ”÷ADG£¬µĆ³ö¶ŌÓ¦±ßĻąµČCD=GD£¬¼“CG=2CD£¬Ö¤³ö”ĻBAE=”ĻBCG£¬ÓÉASAÖ¤Ć÷”÷ADC”Õ”÷CBG£¬µĆ³öAE=CG=2CD¼“æÉ£®
ĶŲÕ¹ŃÓÉģ£ŗ×÷DG”ĶBC½»CEµÄŃÓ³¤ĻßÓŚG£¬Ķ¬ÉĻÖ¤Ć÷Čż½ĒŠĪČ«µČ£¬µĆ³öDF=CG¼“æÉ£®
¢ŁĶ¼1ÖŠĖłÓŠµÄČ«µČČż½ĒŠĪĪŖ”÷ABE”Õ”÷ACE£¬”÷ADF”Õ”÷CDB£»¹Ź“š°øĪŖ£ŗ”÷ABE”Õ”÷ACE£¬”÷ADF”Õ”÷CDB
¢ŚĻ߶ĪAFÓėĻ߶ĪCEµÄŹżĮæ¹ŲĻµŹĒ£ŗAF=2CE£»¹Ź“š°øĪŖ£ŗAF=2CE£®
ĪŹĢāĢ½¾æ£ŗ
Ö¤Ć÷£ŗŃÓ³¤AB”¢CD½»ÓŚµćG£¬ČēĶ¼2ĖłŹ¾£ŗ

”ßADĘ½·Ö”ĻBAC£¬
”ą”ĻCAD=”ĻGAD£¬
”ßAD”ĶCD£¬
”ą”ĻADC=”ĻADG=90”ć£¬
ŌŚ”÷ADCŗĶ”÷ADGÖŠ£¬
![]()
 £¬
£¬
”ą”÷ADC”Õ”÷ADG£ØASA£©£¬
”ąCD=GD£¬¼“CG=2CD£¬
”ß”ĻBAC=45”ć£¬AB=BC£¬
”ą”ĻABC=90”ć£¬
”ą”ĻCBG=90”ć£¬
”ą”ĻG+”ĻBCG=90”ć£¬
”ß”ĻG+”ĻBAE=90”ć£¬
”ą”ĻBAE=”ĻBCG£¬
ŌŚ”÷ABEŗĶ”÷CBGÖŠ£¬
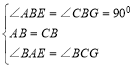 £¬
£¬
”ą”÷ADC”Õ”÷CBGÖŠ£ØASA£©£¬
”ąAE=CG=2CD£®
ĶŲÕ¹ŃÓÉģ£ŗ
½ā£ŗ×÷DG”ĶBC½»CEµÄŃÓ³¤ĻßÓŚG£¬
ČēĶ¼3ĖłŹ¾£®



 ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø
ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬·½øńÖ½ÖŠµÄĆæøöŠ”·½øń¶¼ŹĒ±ß³¤ĪŖ1øöµ„Ī»µÄÕż·½ŠĪ£¬ŌŚ½ØĮ¢Ę½ĆęÖ±½Ē×ų±źĻµŗó£¬![]() µÄ¶„µć¾łŌŚøńµćÉĻ£¬µć
µÄ¶„µć¾łŌŚøńµćÉĻ£¬µć![]() µÄ×ų±źĪŖ
µÄ×ų±źĪŖ![]() £®
£®

¢Ł°Ń![]() ĻņÉĻĘ½ŅĘ5øöµ„Ī»ŗóµĆµ½¶ŌÓ¦µÄ
ĻņÉĻĘ½ŅĘ5øöµ„Ī»ŗóµĆµ½¶ŌÓ¦µÄ![]() £¬»³ö
£¬»³ö![]() £¬²¢Š“³ö
£¬²¢Š“³ö![]() µÄ×ų±ź£»
µÄ×ų±ź£»
¢ŚŅŌŌµć![]() ĪŖ¶Ō³ĘÖŠŠÄ£¬»³ö
ĪŖ¶Ō³ĘÖŠŠÄ£¬»³ö![]() Óė¹ŲÓŚŌµć
Óė¹ŲÓŚŌµć![]() ¶Ō³ĘµÄ
¶Ō³ĘµÄ![]() £¬²¢Š“³öµć
£¬²¢Š“³öµć![]() µÄ×ų±ź£®
µÄ×ų±ź£®
¢ŪŅŌŌµćOĪŖŠż×ŖÖŠŠÄ£¬»³ö°Ń![]() Ė³Ź±ÕėŠż×Ŗ90”ćµÄĶ¼ŠĪ”÷A3B3C3£¬²¢Š“³öC3µÄ×ų±ź£®
Ė³Ź±ÕėŠż×Ŗ90”ćµÄĶ¼ŠĪ”÷A3B3C3£¬²¢Š“³öC3µÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
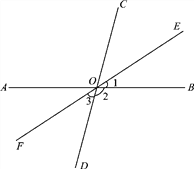
”¾ĢāÄæ”æČēĶ¼£¬Ö±ĻßAB”¢CDĻą½»ÓŚµćO£¬”ĻBOC£½80”ć£¬OEŹĒ”ĻBOCµÄ½ĒĘ½·ÖĻߣ¬OFŹĒOEµÄ·“ĻņŃÓ³¤Ļߣ®
£Ø1£©Ēó”Ļ2”¢”Ļ3µÄ¶ČŹż£»
£Ø2£©ĖµĆ÷OFĘ½·Ö”ĻAODµÄĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijÉĢ³”¾ĻśŅ»ÖÖÉĢĘ·£¬ŅŃÖŖĘäĆ漞½ų¼ŪĪŖ40ŌŖ”£ĻÖŌŚĆ漞ŹŪ¼ŪĪŖ70ŌŖ£¬ĆæŠĒĘŚæÉĀō³ö500¼ž”£øĆÉĢ³”ĶعżŹŠ³”µ÷²é·¢ĻÖ£ŗČōĆ漞ÕĒ¼Ū1ŌŖ£¬ŌņĆæŠĒĘŚÉŁĀō³ö10¼ž£»ČōĆ漞½µ¼Ū1ŌŖ£¬ŌņĆæŠĒĘŚ¶ąĀō³öm£ØmĪŖÕżÕūŹż£©¼ž”£Éčµ÷²é¼ŪøńŗóĆæŠĒĘŚµÄĻśŹŪĄūČóĪŖWŌŖ”£
£Ø1£©ÉčøĆÉĢĘ·Ć漞ÕĒ¼Ūx£ØxĪŖÕżÕūŹż£©ŌŖ£¬
¢ŁČōx£½5£¬ŌņĆæŠĒĘŚæÉĀō³ö____¼ž£¬ĆæŠĒĘŚµÄĻśŹŪĄūČóĪŖ_____ŌŖ£»
¢Śµ±xĪŖŗĪÖµŹ±£¬W×ī“ó£¬WµÄ×ī“óÖµŹĒ¶ąÉŁ”£
£Ø2£©ÉčøĆÉĢĘ·Ć漞½µ¼Ūy£ØyĪŖÕżÕūŹż£©ŌŖ£¬
¢ŁŠ“³öWÓėYµÄŗÆŹż¹ŲĻµŹ½£¬²¢Ķعż¼ĘĖćÅŠ¶Ļ£ŗµ±m£½10Ź±ĆæŠĒĘŚĻśŹŪĄūČóÄÜ·ń“ļµ½£Ø1£©ÖŠWµÄ×ī“óÖµ£»
¢ŚČōŹ¹y£½10Ź±£¬ĆæŠĒĘŚµÄĻśŹŪĄūČóW×ī“ó£¬Ö±½ÓŠ“³öWµÄ×ī“óÖµĪŖ_____”£
£Ø3£©ČōĆ漞½µ¼Ū5ŌŖŹ±µÄĆæŠĒĘŚĻśŹŪĄūČ󣬲»µĶÓŚĆ漞ÕĒ¼Ū15ŌŖŹ±µÄĆæŠĒĘŚĻśŹŪĄūČó£¬ĒómµÄȔֵ·¶Ī§”£
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
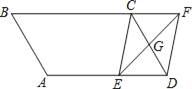
”¾ĢāÄæ”æČēĶ¼£¬ABCDÖŠ£¬GŹĒCDµÄÖŠµć£¬EŹĒ±ß³¤ADÉĻµÄ¶Æµć£¬EGµÄŃÓ³¤ĻßÓėBCµÄŃÓ³¤ĻßĻą½»ÓŚµćF£¬Į¬½ÓCE£¬DF£®
£Ø1£©ĒóÖ¤£ŗĖıߊĪCEDFŹĒĘ½ŠŠĖıߊĪ£®
£Ø2£©ĢīæÕ£ŗČōAB£½3cm£¬BC£½5cm£¬”ĻB£½60”ć£¬Ōņ¢Łµ±AE£½”” ””Ź±£¬ĖıߊĪCEDFŹĒ¾ŲŠĪ£»¢Śµ±AE£½”” ””Ź±£¬ĖıߊĪCEDFŹĒĮāŠĪ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬EF”ĶAD£¬½«Ę½ŠŠĖıߊĪABCDŃŲ×ÅEF¶ŌÕŪ£®Éč”Ļ1µÄ¶ČŹżĪŖn”ć£¬Ōņ”ĻC=______£®£ØÓĆŗ¬ÓŠnµÄ“śŹżŹ½±ķŹ¾£©

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
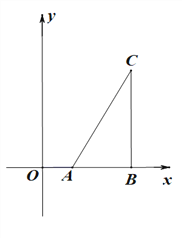
”¾ĢāÄæ”æŅŃÖŖA£Ø2,0£©£¬B£Ø6,0£©£¬CB”ĶxÖįÓŚµćB£¬Į¬½ÓAC
»Ķ¼²Ł×÷£ŗ
£Ø1£©ŌŚyÕż°ėÖįÉĻĒó×÷µćP£¬Ź¹µĆ”ĻAPB=”ĻACB£Ø³ß¹ę×÷Ķ¼£¬±£Įō×÷Ķ¼ŗŪ¼££©
Ąķ½āÓ¦ÓĆ£ŗ
£Ø2£©ŌŚ£Ø1£©µÄĢõ¼žĻĀ£¬
¢ŁČōtan”ĻAPB ![]() £¬ĒóµćPµÄ×ų±ź
£¬ĒóµćPµÄ×ų±ź
¢Śµ±µćPµÄ×ų±źĪŖ Ź±£¬”ĻAPB×ī“ó
ĶŲÕ¹ŃÓÉģ£ŗ
£Ø3£©ČōŌŚÖ±Ļßy![]() x+4ÉĻ“ęŌŚµćP£¬Ź¹µĆ”ĻAPB×ī“ó£¬ĒóµćPµÄ×ų±ź
x+4ÉĻ“ęŌŚµćP£¬Ź¹µĆ”ĻAPB×ī“ó£¬ĒóµćPµÄ×ų±ź
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¹ÉĆńŠ”ŗśÉĻŠĒĘŚĪåŅŌĆæ¹É13.1ŌŖµÄ¼ŪøńĀņ½ųijÖÖ¹Éʱ1000¹É£¬øĆ¹Éʱ±¾ÖܵÄÕĒµųĒéæö(±ķøńŹż×Ö±ķŹ¾±ČĒ°--ĢģÕĒ»ņµų¶ąÉŁŌŖ)ČēĻĀ±ķ(µ„Ī»:ŌŖ):
ŠĒĘŚ | Ņ» | ¶ž | Čż | ĖÄ | Īå |
Ćæ¹ÉÕĒµų | -0.3 | 0 | -0.1 | +0.2 | +0.1 |
(1)±¾ÖÜÄŚ×īøß¼ŪŹĒĆæ¹É__________ŌŖ×īµĶ¼ŪŹĒĆæ¹ÉŌŖ_________£»
(2)Čē¹ūŠ”ŗśŌŚŠĒĘŚĪåŹÕÅĢĒ°½«Č«²æ¹ÉʱĀō³ö£¬ĖūµÄŹÕŅęĒéæöČēŗĪ?
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”涞“ĪŗÆŹży=ax2+bx+c£Øa”Ł0£©µÄ²æ·ÖĶ¼ĻóČēĶ¼ĖłŹ¾£¬Ę䶄µć×ų±źĪŖ£Ø1£¬n£©£¬ĒŅÓėxÖįµÄŅ»øö½»µćŌŚ£Ø3£¬0£©ŗĶ£Ø4£¬0£©Ö®¼ä£¬ŌņĻĀĮŠ½įĀŪ£ŗ
¢Łac![]()
¢Śa©b+c£¾0£»
¢Ūµ±![]() Ź±£¬yĖęxµÄŌö“ó¶ųŌö“ó
Ź±£¬yĖęxµÄŌö“ó¶ųŌö“ó
Čō£Ø©![]() £¬y1£©£¬£Ø
£¬y1£©£¬£Ø![]() £¬y2£©ŹĒÅ×ĪļĻßÉĻµÄĮ½µć£¬Ōņy1
£¬y2£©ŹĒÅ×ĪļĻßÉĻµÄĮ½µć£¬Ōņy1![]() y2£»
y2£»
¢ÜŅ»ŌŖ¶ž“Ī·½³Ģax2+bx+c=n©1ÓŠĮ½øö²»ĻąµČµÄŹµŹżøł£®
ĘäÖŠÕżČ·½įĀŪµÄøöŹżŹĒ£Ø””””£©
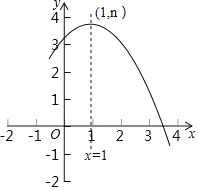
A. 1 B. 2 C. 3 D. 4
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com