练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】观察如图所示的长方体.

    (1)用符号表示下列两棱的位置关系：AB___A′B′，AA′_____AB，D′A′_____D′C′，AD______BC.

    (2) A′B′与BC所在的直线是两条不相交的直线，它们_____平行线.（填“是”或“不是”）

    【答案】(1)∥； ⊥； ⊥； ∥； (2)不是.

    【解析】

    （1）根据长方体的性质进行填空；
    （2）根据平行线的定义进行填空．

    解：（1）如图，在矩形ABB1A1中，AB∥A′B′，AA′⊥AB；
    在矩形A′B′C′D′中，D′A′⊥D′C′；
    在矩形ABCD中，AD∥BC．
    故答案分别是：∥，⊥，⊥，∥；（2）根据图示知，直线A′B′与BC不在同一平面内，所以它们虽然没有交点，但是它们也不平行．
    故答案是：不是．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】若关于y的一元二次方程ky2﹣4y﹣3=3y+4有实根，则k的取值范围是（ ）
    A.k＞﹣
    B.k≥﹣ 且k≠0
    C.k≥﹣
    D.k＞ 且k≠0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中AB＝15，AC＝13，高AD＝12，求BC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：一次函数y＝（3﹣m）x+m﹣5．

    （1）若一次函数的图象过原点，求实数m的值；

    （2）当一次函数的图象经过第二、三、四象限时，求实数m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数y=ax2+bx+c（a、b、c为常数且a≠0）中的x与y的部分对应值如下表：

    x

    ﹣3

    ﹣2

    ﹣1

    0

    1

    2

    3

    4

    5

    y

    12

    5

    0

    ﹣3

    ﹣4

    ﹣3

    0

    5

    12

    给出了结论：
    ⑴二次函数y=ax2+bx+c有最小值，最小值为﹣3；
    ⑵当 时，y＜0；
    ⑶二次函数y=ax2+bx+c的图象与x轴有两个交点，且它们分别在y轴两侧．则其中正确结论的个数是（ ）
    A.3
    B.2
    C.1
    D.0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】平面镜反射光线的规律：射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等．如图①，一束光线m射到平面镜a上，被a反射后的光线为n，则入射光线m、反射光线n与平面镜a所夹的锐角相等，即∠1＝∠2.

    如图②所示，AB，CD为两面平面镜，经过两次反射后，入射光线m与反射光线n之间的位置关系会随之改变，请你计算：图②中，当两平面镜AB，CD的夹角∠ABC是多少度时，可以使入射光线m与反射光线n平行但方向相反．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

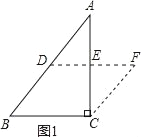
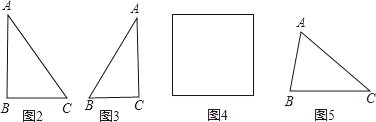
    【题目】在△ABC中，沿图示的中位线DE剪一刀，拼成如图1所示的平行四边形BCFD．请仿上述方法，按要求完成下列操作设计，并在规定位置画出图示：

    （1）在△ABC中，若∠C＝90°，沿着中位线剪一刀，可拼成矩形或等腰梯形，请将拼成的图形画在图2位置（只需画一个）；

    （2）在△ABC中，若AB＝2BC，沿着中位线剪一刀，可拼成菱形，并将拼成的图形画在图3位置；

    （3）在△ABC中，需增加什么条件，沿着中位线剪一刀，拼成正方形，并将拼成的图形和符合条件的三角形一同画在图4位置；

    （4）在△ABC中，若沿着某条线剪一刀，能拼成等腰梯形，请将拼成的图形画在图5位置（保留寻求剪裁线的痕迹）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=ax2+bx+4与x轴交于A（﹣2，0）、B（4、0）两点，与y轴交于C点．

    （1）求抛物线的解析式；
    （2）T是抛物线对称轴上的一点，且△ATC是以AC为底的等腰三角形，求点T的坐标；
    （3）M、Q两点分别从A、B点以每秒1个单位长度的速度沿x轴同时出发相向而行，当点M到原点时，点Q立刻掉头并以每秒 个单位长度的速度向点B方向移动，当点M到达抛物线的对称轴时，两点停止运动，过点M的直线l⊥x轴交AC或BC于点P．求点M的运动时间t与△APQ面积S的函数关系式，并求出S的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

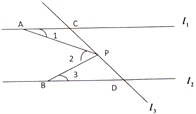
    【题目】如图，已知直线，直线和直线交于点和点，为直线上的一点，，分别是直线，上的定点．

    （1）若点在线段（、两点除外）上运动时，问、、之间的关系是什么？这种关系是否发生变化？请说明理由；

    （2）若在线段之外时，、、的关系又怎样？说明理由．

    查看答案和解析>>

    同步练习册答案