

| GH+CE |
| 2 |
| 6+12 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|
| 2 |
| 2 |
6+12-6
| ||
| 2 |
| 2 |



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 用对角线把多边形分成几个三角形,叫做“多边形的三角剖分”.如图,凸四边形ABCD,有两种剖分方法:(如图示)20世纪,数学家乌尔班发现并证明了下面的公式:
用对角线把多边形分成几个三角形,叫做“多边形的三角剖分”.如图,凸四边形ABCD,有两种剖分方法:(如图示)20世纪,数学家乌尔班发现并证明了下面的公式:| Dn+1 |
| Dn |
| 4n-6 |
| n |
查看答案和解析>>
科目:初中数学 来源:2011-2012学年山东省德州市育英中学初三中考模拟考试数学卷.doc 题型:解答题
(本题满分12分)提出问题:如图,有一块分布均匀的等腰三角形蛋糕( ,且
,且 ),在蛋糕的边缘均匀分布着巧克力,小明和小华决定只切一刀将这块蛋糕平分(要求分得的蛋糕和巧克力质量都一样).
),在蛋糕的边缘均匀分布着巧克力,小明和小华决定只切一刀将这块蛋糕平分(要求分得的蛋糕和巧克力质量都一样).
背景介绍:这条分割直线即平分了三角形的面积,又平分了三角形的周长,我们称这条线为三角 形的“等分积周线”.
尝试解决: (1)小明很快就想到了一条分割直线,而且用尺规作图作出.请你帮小明在图1中画出这条“等分积周线”,从而平分蛋糕.
(1)小明很快就想到了一条分割直线,而且用尺规作图作出.请你帮小明在图1中画出这条“等分积周线”,从而平分蛋糕.
(2) 小华觉得小明的方法很好,所以自己模仿着在图1中过点C画了一条直线CD交AB于点D.你觉得小华会成功吗?如能成功,说出确定的方法;如不能成功,请说明理由.
(3)通过上面的实践,你一定有了更深刻的认识.请你解决下面的问题:若AB=BC=5 cm,AC=6 cm,请你找出△ABC的所有“等分积周线”,并简要的说明确定的方法.
查看答案和解析>>
科目:初中数学 来源:2014届广东省汕头市七年级第一学期数学整式的加减单元卷 题型:填空题
、用正三角形和正六边形按如图所示的规律拼图案,
即从第二个图案开始,每个图案都比上一个图案多一
个正六边形和两个正三角形,则第 个图案中正三角
个图案中正三角
形的个数为 (用含 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源:2011年福建省泉州市洛江区初二上学期期末数学卷 题型:选择题
如图1,是我国古代数学家赵爽的《勾股弦方图》,它是由四个全等的直角三角
形与中间的小正方形拼成的一个大正方形.如果大正方形的面积是13,小正方形的
面积是1,直角三角形的短直角边为a,较长的直角边为b,那么(a+b)2值为 ( )

A. 169 B. 25 C. 19 D. 13
查看答案和解析>>
科目:初中数学 来源:2010-2011学年北京市考数学一模试卷 题型:选择题
已知:如图,在等边三角形ABC中,M、N分别是AB、AC的中点,D是MN上任意一点,CD、BD的延长线分别与AB、AC交于F、E,若 ,则等边三角
,则等边三角
形ABC的边长为

A. 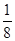 B.
B.  C.
C.
 D.1
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com