
分析 画出图形即可求出点D坐标,再证明四边形ABCD是菱形,求出对角线的长即可解决问题.
解答  解:如图,由图象可知点D坐标为(4,4).
解:如图,由图象可知点D坐标为(4,4).
∵AB=BC=AD=CD=$\sqrt{5}$,
∴四边形ABCD是菱形,
∵AC=$\sqrt{2}$,BD=4$\sqrt{2}$,
∴四边形ABCD面积=$\frac{1}{2}$•BD•AC=$\frac{1}{2}$$•4\sqrt{2}$$•\sqrt{2}$=4.
故答案分别为(4,4),4.
点评 本题考查平行四边形的性质、菱形的判定和性质、勾股定理等知识,解题的关键是正确画出图形,记住菱形的面积公式=对角线乘积的一半,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
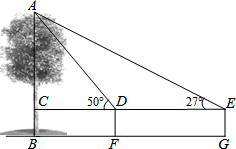 某数学兴趣小组用高为1.2米的测角仪测量小树AB的高度,如图,在距AB一定距离的F处测得小树顶部A的仰角为50°,沿BF方向行走3.5米到G处时,又测得小树顶部A的仰角为27°,求小树AB的高度.(参考数据:sin27°=0.45,cos27°=0.89,tan27°=0.5,sin50°=0.77,cos50°=0.64,tan50°=1.2)
某数学兴趣小组用高为1.2米的测角仪测量小树AB的高度,如图,在距AB一定距离的F处测得小树顶部A的仰角为50°,沿BF方向行走3.5米到G处时,又测得小树顶部A的仰角为27°,求小树AB的高度.(参考数据:sin27°=0.45,cos27°=0.89,tan27°=0.5,sin50°=0.77,cos50°=0.64,tan50°=1.2)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知:平行四边形ABCD,点E在AD上,且BE平分∠ABC,CE平分∠BCD,tan∠EBC=$\frac{1}{2}$,BE=4,则△CDE的面积为$\frac{6}{5}$.
已知:平行四边形ABCD,点E在AD上,且BE平分∠ABC,CE平分∠BCD,tan∠EBC=$\frac{1}{2}$,BE=4,则△CDE的面积为$\frac{6}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=$\frac{3}{x}$ | B. | y=$\frac{2}{x}$ | C. | y=$\frac{6}{x}$ | D. | y=3x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在梯形ABCD中,AD∥BC,且AD∥BC,AB=8cm,AD=20cm,BC=22cm,点P、Q分别从A、C同时出发,P以2cm/s的速度由A向D运动,点Q以3cm/s的速度由C出发向B运动.
在梯形ABCD中,AD∥BC,且AD∥BC,AB=8cm,AD=20cm,BC=22cm,点P、Q分别从A、C同时出发,P以2cm/s的速度由A向D运动,点Q以3cm/s的速度由C出发向B运动.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com