练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．某中学课外兴趣活动小组准备围建一个矩形苗圃园，其中一边靠墙，另外三边周长为30米的篱笆围成．已知墙长为18米（如图所示），设这个苗圃园垂直于墙的一边长为x米．若苗圃园的面积为72平方米，求x的值．

    分析 根据题意可以列出相应的一元二次方程，从而可以解答本题．

    解答 解：设这个苗圃园垂直于墙的一边长为x米，则圃园与墙平行的一边长为（30-2x）米，
    x（30-2x）=72，
    即x2-15x+36=0，
    解得，x1=3（舍去），x2=12，
    即x的值是12．

    点评 本题考查一元二次方程的应用，解题的关键是明确题意，找出所求问题需要的条件．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    9．若m，n满足|m-3|+（2n+4）2=0，求-mn2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

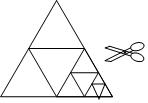    10．如图，将一张等边三角形纸片沿中位线剪成4个小三角形，称为第一次操作；然后，将其中的一个三角形按同样方式再剪成4个小三角形，共得到7个小三角形，称为第二次操作；再将其中一个三角形按同样方式再剪成4个小三角形，共得到10个小三角形，称为第三次操作；…根据以上操作，若要得到100个小三角形，则需要操作的次数是33．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．设点A（-1，a）和点B（4，b）在直线y=-x+m上，则a与b的大小关系是（　　）
    A．a＞bB．a＜bC．a=bD．无法确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．例：解方程x4-7x2+12=0
    解：设x2=y，则x4=y2，∴原方程可化为：y2-7y+12=0，解得y1=3，y2=4，
    当y=3时，x2=3，x=±$\sqrt{3}$，当y=4时，x2=4，x=±2．
    ∴原方程有四个根是：x1=$\sqrt{3}$，x2=-$\sqrt{3}$，x3=2，x4=-2．
    以上方法叫换元法，达到了降次的目的，体现了数学的转化思想，运用上述方法解答下列问题．
    （1）解方程：（x2+x-2）（x2+x-3）=2；
    （2）已知a、b、c是Rt△ABC的三边（c为斜边），S△ABC=6，且a、b满足（a2+b2）2-21（a2+b2）-100=0，试求Rt△ABC的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．计算：
    （1）（-$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{5}$）×20
    （2）-13-（1+0.5）×$\frac{1}{3}$÷（-4）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．某商场销售一种西装和领带，西装每套定价1000元，领带每条定价200元．元旦打折
    方案一：买一套西装送一条领带；
    方案二：西装和领带都按定价的90%付款．
    现某客户要到该商场购买西装20套，领带x条（x＞20）．
    （1）若该客户按方案一购买，需付款200x+16000元．（用含x的代数式表示）
    若该客户按方案二购买，需付款180x+18000 元．（用含x的代数式表示）
    （2）若x等于30，通过计算说明此时按哪种方案更合算．
    （3）当x=30，你能给出一种更为省钱的购买方案吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．水果店张阿姨以每斤2元的价格购进某种水果若干斤，然后以每斤4元的价格出售，每天可售出100斤．通过调查发现，这种水果每斤的售价每降低0.1元，每天可多售出20斤，为保证每天至少售出260斤，张阿姨决定降价销售．
    （1）当售价降低0.5元时，计算每天的销售量和销售利润．
    （2）若将这种水果的售价降低x元，则每天的销售量是（100+200x）斤（用含x的代数式表示）
    （3）销售这种水果要想每天获得300元的利润，张阿姨将每斤的售价降低多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．如图1是长方形纸带，∠DEF=10°，将纸带沿EF折叠成图2，再沿BF折叠成图3，则图3中∠CFE度数是多少（　　）
    A．160°B．150°C．120°D．110°

    查看答案和解析>>

    同步练习册答案