
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc>0;②b<a+c;③4a+2b+c>0;④b2﹣4ac>0;其中正确的结论有( ) 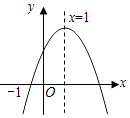
A.1个
B.2个
C.3个
D.4个
【答案】B
【解析】解:①∵抛物线开口向下, ∴a<0.
∵抛物线的对称轴为x=﹣ ![]() =1,
=1,
∴b=﹣2a>0.
当x=0时,y=c>0,
∴abc<0,①错误;
②当x=﹣1时,y<0,
∴a﹣b+c<0,
∴b>a+c,②错误;
③∵抛物线的对称轴为x=1,
∴当x=2时与x=0时,y值相等,
∵当x=0时,y=c>0,
∴4a+2b+c=c>0,③正确;
④∵抛物线与x轴有两个不相同的交点,
∴一元二次方程ax2+bx+c=0,
∴△=b2﹣4ac>0,④正确.
综上可知:成立的结论有2个.
故选B.
由抛物线的开口方程、抛物线的对称轴以及当x=0时的y值,即可得出a、b、c的正负,进而即可得出①错误;由x=﹣1时,y<0,即可得出a﹣b+c<0,进而即可得出②错误;由抛物线的对称轴为x=1结合x=0时y>0,即可得出当x=2时y>0,进而得出4a+2b+c=c>0,③成立;由二次函数图象与x轴交于不同的两点,结合根的判别式即可得出△=b2﹣4ac>0,④成立.综上即可得出结论.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[﹣2.5]=﹣3;用<a>表示大于a的最小整数,例如:<2.5>=3,<4>=5,<﹣1.5>=﹣1.解决下列问题:
(1)[﹣4.5]= , <3.5>= .
(2)若[x]=2,则x的取值范围是;若<y>=﹣1,则y的取值范围是 .
(3)已知x,y满足方程组 ![]() ,求x,y的取值范围.
,求x,y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直角三角形![]() 中,
中,![]() ,直线
,直线![]() 过点
过点![]() .
.
(1)当![]() 时,如图1,分别过点
时,如图1,分别过点![]() 和
和![]() 作
作![]() 直线
直线![]() 于点
于点![]() ,
,![]() 直线
直线![]() 于点
于点![]() .
.![]() 与
与![]() 是否全等,并说明理由;
是否全等,并说明理由;
(2)当![]() ,
,![]() 时,如图2,点
时,如图2,点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,连接
对称,连接![]() 、
、![]() .点
.点![]() 是
是![]() 上一点,点
上一点,点![]() 是
是![]() 上一点,分别过点
上一点,分别过点![]() 、
、![]() 作
作![]() 直线
直线![]() 于点
于点![]() ,
,![]() 直线
直线![]() 于点
于点![]() ,点
,点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 的速度沿
的速度沿![]() 路径运动,终点为
路径运动,终点为![]() .点
.点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 的速度沿
的速度沿![]() 路径运动,终点为
路径运动,终点为![]() .点
.点![]() 、
、![]() 同时开始运动,各自达到相应的终点时停止运动,设运动时间为
同时开始运动,各自达到相应的终点时停止运动,设运动时间为![]() 秒.
秒.
①当![]() 为等腰直角三角形时,求
为等腰直角三角形时,求![]() 的值;
的值;
②当![]() 与
与![]() 全等时,求
全等时,求![]() 的值.
的值.


图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课本的作业题中有这样一道题:把一张顶角为36°的等腰三角形纸片剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形,你能办到吗?请画示意图说明剪法.

我们有多少种剪法,图1是其中的一种方法:定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.
请你在图2中用三种不同的方法画出顶角为45°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数;(若两种方法分得的三角形成3对全等三角形,则视为同一种)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB是⊙O的直径,CE平分∠ACB交⊙O于点E,∠E=30°,交AB于点D,连接AE,则SADC:S△ADE的比值为( ) 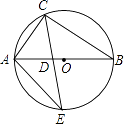
A.![]()
B.![]()
C.![]()
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
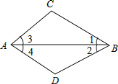
【题目】如图,除公共边![]() 外,根据下列括号内三角形全等的条件,在横线上添加适当的条件,使
外,根据下列括号内三角形全等的条件,在横线上添加适当的条件,使![]() 与
与![]() 全等:
全等:
![]() ________,________
________,________![]() ;
;
![]() ________,________
________,________![]() ;
;
![]() ,________
,________![]() ;
;
![]() ________,
________,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C,D在⊙O上,点O在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=( ) 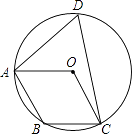
A.55°
B.60°
C.65°
D.70°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com