
分析 (1)根据根的判别式,可得答案;
(2)根据待定系数法,可得函数解析式,根据自变量与函数值的对应关系,可得B、C坐标,
①根据线段垂直平分线的性质,可得DC=DB,根据勾股定理,可得答案;
②根据平行四边形的对边相等,可得关于m的方程,解方程,可得答案.
解答 (1)证明:y=x2-2ax-2a-6
当a≠0时,(-2a)2-4(-2a-6)=4a2+8a+24=4(a+1)2+20
∵4(a+1)2≥0
∴4(a+1)2+20>0
所以,该函数的图象与x轴总有两个公共点.
(2)①如图1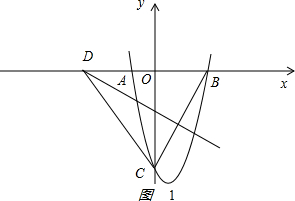 ,
,
把(-2,0)代入y=x2-2ax-2a-6得a=1
所以,y=x2-2x-8.
当x=0时,y=-8,即C(0,-8),当y时,x2-2x-8=0,解得x=2(不符合题意,舍),x=4,即B(4,0),
B(4,0)、C(0,-8)
∵点D在BC的垂直平分线上
∴DC=DB
设OD=x,则DC=DB=x+4,
在Rt△ODC中 OD2+OC2=DC2,
即x2+82=(x+4)2,
解得x=6
所以D(-6,0)
②Q1($\frac{23}{2}$,-$\frac{35}{4}$)、Q2(10,-8)、Q3(-$\frac{25}{2}$,$\frac{13}{4}$)、Q4($\frac{1}{2}$,-$\frac{13}{4}$).
设BC的中点为E,则点E (2,-4),
直线l的函数关系式为y=-$\frac{1}{2}$x-3,
以点B、D、P、Q为顶点的四边形分以下两种情况讨论
第一种情况:当DB为四边形的边时,如图2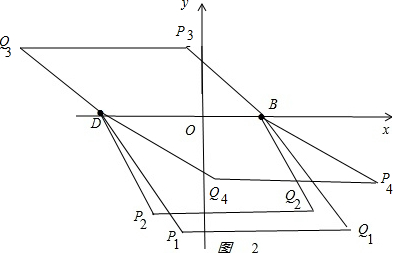 ,
,
当PQ∥DB且PQ=DB时,四边形DPQB为平行四边形,
若PQ在x轴下方时,设点Q(m,-$\frac{1}{2}$m-3)则P(m-10,-$\frac{1}{2}$m-3),
因为点P在抛物线上,所以-$\frac{1}{2}$m-3=(m-10)2-2(m-10)-8.
解得m1=$\frac{23}{2}$,m2=10
所以Q1($\frac{23}{2}$,-$\frac{35}{4}$)、Q2(10,-8)
若PQ在x轴上方时,设点Q(m,-$\frac{1}{2}$m-3)则P(m+10,-$\frac{1}{2}$m-3)
因为点P在抛物线上,所以-$\frac{1}{2}$m-3=(m+10)2-2(m+10)-8.
解得m1=-$\frac{25}{2}$,m2=-6(舍去)
所以Q3(-$\frac{25}{2}$,$\frac{13}{4}$)
第二种情况:当DB为四边形的对角线时
当DQ4∥PB且DQ4=PB时,四边形D Q4BP为平行四边形
此时可发现DQ4=PB=DQ3,即D为Q3Q4的中点
所以,可求出Q4点($\frac{1}{2}$,-$\frac{13}{4}$).
点评 本题考查了二次函数综合题,利用根的判别式是解题关键;利用勾股定理得出关于m的方程是解题关键,利用平行四边形的对边相等得出关于m的方程是解题关键.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:选择题
 如图,已知点D、E分别在△ABC边AB、AC上,DE∥BC,BD=2AD,那么S△DBE:S△EBC等于( )
如图,已知点D、E分别在△ABC边AB、AC上,DE∥BC,BD=2AD,那么S△DBE:S△EBC等于( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 2:# |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知一次函数y=ax-2的图象与反比例函数y=$\frac{k}{x}$的图象交于A(k,a),B两点.
如图,已知一次函数y=ax-2的图象与反比例函数y=$\frac{k}{x}$的图象交于A(k,a),B两点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
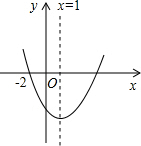 如图所示的抛物线是二次函数y=ax2+bx+c(a≠0)的图象,则下列结论:①b<0;②b+2a=0;③方程ax2+bx+c=0的两个根为x1=-2,x2=4;④a+c>b;⑤3a+c<0.其中正确的结论有( )
如图所示的抛物线是二次函数y=ax2+bx+c(a≠0)的图象,则下列结论:①b<0;②b+2a=0;③方程ax2+bx+c=0的两个根为x1=-2,x2=4;④a+c>b;⑤3a+c<0.其中正确的结论有( )| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
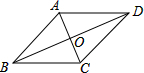 如图,在菱形ABCD中,对角线AC,BD相交于点O,下列结论中不一定成立的是( )
如图,在菱形ABCD中,对角线AC,BD相交于点O,下列结论中不一定成立的是( )| A. | AB∥DC | B. | AC=BD | C. | AC⊥BD | D. | OA=OC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
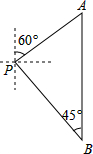 如图,小明从P点出发,沿北偏东60°方向行驶到达A处,接着向正南方向行驶100($\sqrt{3}$+1)米到达B处.在B处观测到出发时所在的P处在北偏西45°方向上,P,A两处相距多少米?
如图,小明从P点出发,沿北偏东60°方向行驶到达A处,接着向正南方向行驶100($\sqrt{3}$+1)米到达B处.在B处观测到出发时所在的P处在北偏西45°方向上,P,A两处相距多少米?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.845×104 | B. | 8.45×103 | C. | 8.45×104 | D. | 84.5×102 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com