
【题目】商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为80元,用180元购进甲种玩具的件数与用300元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共32件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1350元,求商场共有几种进货方案?
【答案】(1)甲、乙两种玩具分别是30元/件、50元/件;(2)共有3种方案
【解析】
(1)设甲种玩具的进价为x元/件,则乙种玩具的进价为(80-x)元/件,根据数量=总价÷单价结合用180元购进甲种玩具的件数与用300元购进乙种玩具的件数相同,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)设购进甲种玩具y件,则购进乙种玩具(32-y)件,根据甲种玩具的件数少于乙种玩具的件数且进货的总资金不超过1350元,即可得出关于y的一元一次不等式组,解之取其中的整数,即可得出结论.
解:(1)设甲种玩具进价x元/件,则乙种玩具进价为(80﹣x)元/件,
![]() ,
,
解得: ![]() ,
,
经检验![]() 是原方程的解.
是原方程的解.
∴ 80 - 30 = 50.
∴ 甲,乙两种玩具分别是30元/件,和50元/件.
(2)设购进甲种玩具y件,则购进乙种玩具(32﹣y)件,
![]() ,
,
解得:12.5 ≤ y ﹤16 .
∵y只能取整数,
∴ y取13,14,15,
∴ 共有3种方案.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
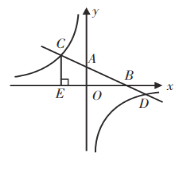
【题目】已知:如图,在平面直角坐标系中,直线![]() 分别与
分别与![]() ,
,![]() 轴交于点
轴交于点![]() ,
,![]() ,与反比例函数的图象分别交于点
,与反比例函数的图象分别交于点![]() ,
,![]() ,
, ![]() 轴于点
轴于点![]() ,
, ![]() ,
,![]() ,
,![]() .
.
(1)求![]() 的长;
的长;
(2)求反比例函数的解析式;
(3)连接![]() ,求
,求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在近期“抗疫”期间,某药店销售A、B两种型号的口罩,已知销售800只A型和450只B型的利润为210元,销售400只A型和600只B型的利润为180元.
(1)求每只A型口罩和B型口罩的销售利润;
(2)该药店计划一次购进两种型号的口罩共2000只,其中B型口罩的进货量不超过A型口罩的3倍,设购进A型口罩x只,这2000只口罩的销售总利润为y元.
①求y关于x的函数关系式;
②该药店购进A型、B型口罩各多少只,才能使销售总利润最大?
(3)在销售时,该药店开始时将B型口罩提价100%,当收回成本后,为了让利给消费者,决定把B型口罩的售价调整为进价的15%,求B型口罩降价的幅度.
查看答案和解析>>
科目:初中数学 来源: 题型:
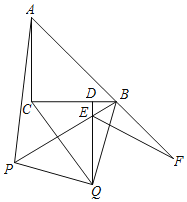
【题目】如图,已知△ABC中,AC=BC,∠ACB=90°,将△ABC绕点B逆时针方向旋转得到△PBQ,旋转角为α,且45°<α<90°.
(1)连接AP,CQ,则![]() = ;
= ;
(2)若QD⊥BC,垂足为点D,∠BQD=15°,QD与PB交于点E,∠BEQ的平分线EF交AB的延长线于点F.
①求旋转角α的大小;
②求∠F的度数;
③求证:EQ+EB=EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种高档蔬菜“莼菜”,其进价为16元/kg.经市场调查发现:该商品的日销售量y(kg)是售价x(元/kg)的一次函数,其售价、日销售量对应值如表:
售价 | 20 | 30 | 40 |
日销售量 | 80 | 60 | 40 |
(1)求![]() 关于
关于![]() 的函数解析式(不要求写出自变量的取值范围);
的函数解析式(不要求写出自变量的取值范围);
(2)![]() 为多少时,当天的销售利润
为多少时,当天的销售利润![]() (元)最大?最大利润为多少?
(元)最大?最大利润为多少?
(3)由于产量日渐减少,该商品进价提高了![]() 元/
元/![]() ,物价部门规定该商品售价不得超过36元/
,物价部门规定该商品售价不得超过36元/![]() ,该商店在今后的销售中,日销售量与售价仍然满足(1)中的函数关系.若日销售最大利润是864元,求
,该商店在今后的销售中,日销售量与售价仍然满足(1)中的函数关系.若日销售最大利润是864元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一辆汽车在高速公路上行驶的平均速度比在普通公路上行驶的平均速度提高80%,那么行驶81千米的高速公路比行驶同等长度的普通公路所用时间将会缩短36分钟,求该汽车在高速公路上行驶的平均速度是多少千米∕小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
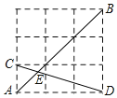
【题目】如图,在由边长为1的小正方形组成的网格中.点 A,B,C,D 都在这些小正方形的格点上,AB、CD 相交于点E,则sin∠AEC的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个口袋中装有7个只有颜色不同的球,其中3个白球,4个黑球.
(1)求从中随机抽取出一个黑球的概率是多少?
(2)若往口袋中再放入x个白球和y个黑球,从口袋中随机取出一个白球的概率是![]() ,求y与x之间的函数关系式;
,求y与x之间的函数关系式;
(3)若在(2)的条件下,放入白球x的范围是0<x<4(x为整数),求y的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
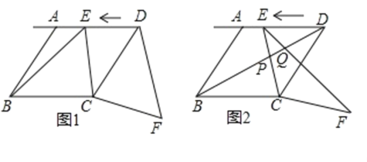
【题目】如图1,在菱形ABCD中,AB=5,tan∠ABC=![]() ,点E从点D出发,以每秒1个单位长度的速度沿着射线DA的方向匀速运动,设运动时间为t(秒),将线段CE绕点C顺时针旋转一个角α(α=∠BCD),得到对应线段CF.
,点E从点D出发,以每秒1个单位长度的速度沿着射线DA的方向匀速运动,设运动时间为t(秒),将线段CE绕点C顺时针旋转一个角α(α=∠BCD),得到对应线段CF.
(1)求证:BE=DF;
(2)当t=___秒时,DF的长度有最小值,最小值等于___;
(3)如图2,连接BD、EF、BD交EC、EF于点P、Q,当t为何值时,△EPQ是直角三角形?
(4)在点E的运动过程中,是否存在到直线AD的距离为1的点F,若存在直接写出 t的值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com